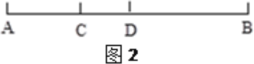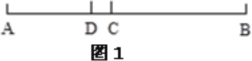��Ŀ����
����Ŀ����ͼ����������A��B��C�����㣬���DZ�ʾ�����ֱ���![]() ��
��![]() ��
��![]() ��
��

��1����գ�AB�� ��BC�� ��
��2�����ж���M��N����A���������M��ÿ��2����λ���ȵ��ٶ������ƶ�������M�ƶ���B��ʱ����N�Ŵ�A�����������ÿ��3����λ���ȵ��ٶ������ƶ������N�ƶ�����ʱ�䣬��N�ϵ�M��
��3������A��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ����B�͵�C�ֱ���ÿ��3����λ���Ⱥ�7����λ���ȵ��ٶ������˶�����̽����BC��AB��ֵ�Ƿ�����ʱ��ı仯���ı䣿��˵�����ɡ�
���𰸡�(1) AB��15��BC��20;(2) ��N�ƶ�15��ʱ����N�ϵ�M;(3) BC��AB��ֵ��������ʱ��ı仯���ı�,���ɼ�����
��������
��1�����������ϵ��λ�����AB��BC�ij�����,
��2������,����Ϊ������t���,A��B��C��������Ӧ�����ֱ���-24-t,-10+3t,10+7t,��ʾ��BC,AB,���BC-AB���������ж�,
��3������t���,��ʾP��Q��������Ӧ����,���������г�����t�ķ���,������̵Ľ�õ�t��ֵ,�������������,�ֱ������������t��ֵ���ɣ�
�⣺��1��AB��15,BC��20,
��2�����N�ƶ�![]() ��ʱ,��N�ϵ�M,������ã�
��ʱ,��N�ϵ�M,������ã�

![]() ,
,
���![]() ,
,
�𣺵�N�ƶ�15��ʱ,��N�ϵ�M.
��3�����˶�ʱ����![]() ��,��ô�˶���A��B��C�����ʾ�����ֱ���
��,��ô�˶���A��B��C�����ʾ�����ֱ���![]() ��
��![]() ��
��![]() ,
,
��BC![]() ,AB
,AB![]() ,
,
��BC��AB![]() ,
,
��BC��AB��ֵ��������ʱ��ı仯���ı�.