题目内容
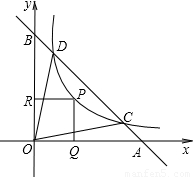
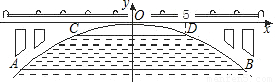
(2003•吉林)如图,直线AB过点A(m,0),B(0,n)(m>0,n>0).反比例函数y=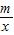 的图象与AB交于C、D两点.P为双曲线y=
的图象与AB交于C、D两点.P为双曲线y= 上任一点,过P作PQ⊥x轴于Q,PR⊥y轴于R.请分别按(1)、(2)、(3)各自的要求解答问题.
上任一点,过P作PQ⊥x轴于Q,PR⊥y轴于R.请分别按(1)、(2)、(3)各自的要求解答问题.(1)若m+n=10,n为何值时△AOB面积最大,最大值是多少?
(2)若S△AOC=S△COD=S△DOB,求n的值;
(3)在(2)的条件下,过O、D、C三点作抛物线,当该抛物线的对称轴为x=1时,矩形PROQ的面积是多少?

【答案】分析:(1)已知了m+n=10,则m=10-n,根据三角形的面积公式即可得出关于S,n的函数关系式,根据函数的性质即可得出S的最大值及对应的n的值.
(2)可根据A、B的坐标求出直线AB的解析式,然后联立反比例函数的解析式得出C、D两点的横坐标,根据等高的三角形的面积比等于底边比以及S△AOC=S△COD=S△DOB,可得出C、D为AB的三等分点,因此C的横坐标为D的横坐标的2倍,由此可求出n的值.
(3)本题的关键是求出m的值,可根据C得到n的值表示出C、D的坐标,已知了抛物线的对称轴为x=1,因此抛物线与x轴的另一交点坐标为(2,0),然后将C、D坐标代入抛物线中,即可求得m的值.而矩形的面积实际是P点横坐标与纵坐标的积,也就是m的值.
解答:解:(1)∵ ,
,
又∵m+n=10,∴
∴ .
.
∴n=5时,△AOB面积最大,最大值为 .
.
(2)分别过D,C作y轴平行线与x轴交于M,N两点,则DM⊥x轴,CN⊥x轴.
由已知得△OBD,△ODC,△OCA等高等底.
∴BD=CD=CA.
又∵BO∥DM∥CN,
∴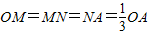 .∴D点的横坐标为
.∴D点的横坐标为 .
.
又∵点D在函数 的图象上,
的图象上,
∴点D纵坐标为 .∴点D坐标为
.∴点D坐标为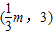 .
.
同样可求得C点坐标为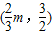 .
.
设直线AB解析式为y=kx+b(k≠0),
把A,B两点坐标代入,得
解得 ∴直线AB解析式为
∴直线AB解析式为 .
.
把D点坐标代入,得 .
.
∵m≠0,
∴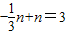 .∴
.∴ .
.
(3)设抛物线解析式为y=ax2+bx+c,
把O,D,C三点坐标分别代入,得
解得 ,
,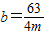 ,c=0.
,c=0.
∴抛物线解析式为 .
.
由已知,得 .
.
解得 或m=0(不合题意,舍去).
或m=0(不合题意,舍去).
设P点坐标为(a,b),
∵点P在双曲线 上,则
上,则 .即ab=m.
.即ab=m.
∴ .
.
点评:本题为二次函数综合题,考查了图形面积的求法、反比例函数、一次函数和二次函数的综合应用、函数图象交点等知识.
(2)可根据A、B的坐标求出直线AB的解析式,然后联立反比例函数的解析式得出C、D两点的横坐标,根据等高的三角形的面积比等于底边比以及S△AOC=S△COD=S△DOB,可得出C、D为AB的三等分点,因此C的横坐标为D的横坐标的2倍,由此可求出n的值.
(3)本题的关键是求出m的值,可根据C得到n的值表示出C、D的坐标,已知了抛物线的对称轴为x=1,因此抛物线与x轴的另一交点坐标为(2,0),然后将C、D坐标代入抛物线中,即可求得m的值.而矩形的面积实际是P点横坐标与纵坐标的积,也就是m的值.
解答:解:(1)∵
 ,
,又∵m+n=10,∴

∴
 .
.∴n=5时,△AOB面积最大,最大值为
 .
.(2)分别过D,C作y轴平行线与x轴交于M,N两点,则DM⊥x轴,CN⊥x轴.

由已知得△OBD,△ODC,△OCA等高等底.
∴BD=CD=CA.
又∵BO∥DM∥CN,
∴
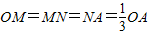 .∴D点的横坐标为
.∴D点的横坐标为 .
.又∵点D在函数
 的图象上,
的图象上,∴点D纵坐标为
 .∴点D坐标为
.∴点D坐标为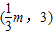 .
.同样可求得C点坐标为
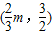 .
.设直线AB解析式为y=kx+b(k≠0),
把A,B两点坐标代入,得

解得
 ∴直线AB解析式为
∴直线AB解析式为 .
.把D点坐标代入,得
 .
.∵m≠0,
∴
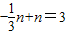 .∴
.∴ .
.(3)设抛物线解析式为y=ax2+bx+c,
把O,D,C三点坐标分别代入,得

解得
 ,
,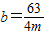 ,c=0.
,c=0.∴抛物线解析式为
 .
.由已知,得
 .
.解得
 或m=0(不合题意,舍去).
或m=0(不合题意,舍去).设P点坐标为(a,b),
∵点P在双曲线
 上,则
上,则 .即ab=m.
.即ab=m.∴
 .
.点评:本题为二次函数综合题,考查了图形面积的求法、反比例函数、一次函数和二次函数的综合应用、函数图象交点等知识.

练习册系列答案
相关题目
 的图象与AB交于C、D两点.P为双曲线y=
的图象与AB交于C、D两点.P为双曲线y= 上任一点,过P作PQ⊥x轴于Q,PR⊥y轴于R.请分别按(1)、(2)、(3)各自的要求解答问题.
上任一点,过P作PQ⊥x轴于Q,PR⊥y轴于R.请分别按(1)、(2)、(3)各自的要求解答问题.

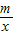 的图象与AB交于C、D两点.P为双曲线y=
的图象与AB交于C、D两点.P为双曲线y=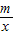 上任一点,过P作PQ⊥x轴于Q,PR⊥y轴于R.请分别按(1)、(2)、(3)各自的要求解答问题.
上任一点,过P作PQ⊥x轴于Q,PR⊥y轴于R.请分别按(1)、(2)、(3)各自的要求解答问题.