题目内容
【题目】为了测量一幢高楼高AB,在旗杆CD与最右边的高楼之间选定一点P.测得旗杆顶C视线PC与地面夹角∠DPC=38°,测楼顶A视线PA与地面夹角∠APB=52°,量得P到楼底距离PB与旗杆CD高度相等,等于8米,量得旗杆与楼之间距离为DB=33米,求楼高AB是多少米?(写出过程)
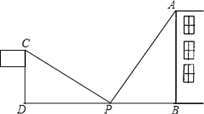
【答案】楼高AB是25米.
【解析】分析:利用全等三角形的判定方法得出△CPD≌△PAB(ASA),而后得出AB的长即可。
本题解析:∵∠CPD=38°,∠APB=52°,∠CDP=∠ABP=90°,
∴∠DCP=∠APB=52°,
在△CPD和△PAB中
∵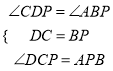 ,
,
∴△CPD≌△PAB(ASA),
∴DP=AB,
∵DB=33,PB=8,
∴AB=33﹣8=25(m),
答:楼高AB是25米.

练习册系列答案
相关题目
【题目】在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如下表所示:
成绩/m | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
人数 | 2 | 3 | 2 | 3 | 4 | 1 |
则这些运动员成绩的中位数、众数分别为( )
A. 1.70,1.75 B. 1.70,1.70
C. 1.65,1.75 D. 1.65,1.70