题目内容
定义一种法则“⊕”如下：a⊕b=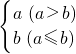
，例如：1⊕2=2，若（-2m-5）⊕3=3，则m的取值范围是________．
m≥-4
分析：先根据题中所给的条件得出关于m的不等式，求出m的取值范围即可．
解答：∵1⊕2=2，若（-2m-5）⊕3=3，
∴-2m-5≤3，解得m≥-4．
故答案为：m≥-4．
点评：本题考查的是解一元一次不等式，根据题意得出关于m的不等式是解答此题的关键．
分析：先根据题中所给的条件得出关于m的不等式，求出m的取值范围即可．
解答：∵1⊕2=2，若（-2m-5）⊕3=3，
∴-2m-5≤3，解得m≥-4．
故答案为：m≥-4．
点评：本题考查的是解一元一次不等式，根据题意得出关于m的不等式是解答此题的关键．
练习册系列答案
53随堂测系列答案
相关题目
，例如：1⊕2=2，若（-2m-5）⊕3=3，则m的取值范围是 ．
，例如：1※2＝2，若
，则
的取值范围是 。