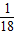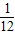题目内容
现掷A、B两枚均匀的小立方体(每个面上分别标有数字1,2,3,4,5,6),设两立方体朝上的数字分别为x、y,并以此确定点P(x,y),那么各掷一次所确定的点P落在已知抛物线y=-x2+4x上的概率为( )A.

B.

C.

D.

【答案】分析:先利用列表展示所有36种等可能的情况,根据二次函数图象上点的坐标特得到(1,3)、(2,4)、(3,3)三个点在抛物线y=-x2+4x上,然后根据概率的定义即可求出点P落在已知抛物线y=-x2+4x上的概率.
解答:解:列表 如下:
如下:
点P共有36种等可能的情况,其中(1,3)、(2,4)、(3,3)三个点在抛物线y=-x2+4x上,
所以它们各掷一次所确定的点P落在已知抛物线y=-x2+4x上的概率为 =
= ,
,
故选B
点评:本题考查了利用列表法与树状图法求概率的方法:先列表展示所有等可能的结果数n,再找出某事件发生的结果数m,然后根据概率的定义计算出这个事件的概率P= ,同时也考查了二次函数图象上点的坐标特征.
,同时也考查了二次函数图象上点的坐标特征.
解答:解:列表
 如下:
如下:点P共有36种等可能的情况,其中(1,3)、(2,4)、(3,3)三个点在抛物线y=-x2+4x上,
所以它们各掷一次所确定的点P落在已知抛物线y=-x2+4x上的概率为
 =
= ,
,故选B
点评:本题考查了利用列表法与树状图法求概率的方法:先列表展示所有等可能的结果数n,再找出某事件发生的结果数m,然后根据概率的定义计算出这个事件的概率P=
 ,同时也考查了二次函数图象上点的坐标特征.
,同时也考查了二次函数图象上点的坐标特征. 
练习册系列答案
相关题目