题目内容
 将直角△ABC绕直角顶点C旋转,使点A落在BC边上的点A′,请你先证明A′B′⊥AB,并利用阴影部分面积完成勾股定理的证明.
将直角△ABC绕直角顶点C旋转,使点A落在BC边上的点A′,请你先证明A′B′⊥AB,并利用阴影部分面积完成勾股定理的证明.已知:如图,在△ABC中,∠ACB=90°,BC=a,AC=b,AB=c.
求证:a2+b2=c2.
证明:作△A′B′C≌△ABC,使点A的对应点A′在边BC上,
连接AA′、BB′,延长B′A′交AB于点M.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
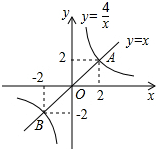 如图,正比例函数y=x与反比例函数y=
如图,正比例函数y=x与反比例函数y=| 4 |
| x |
| 4 |
| x |
| A、x>2 |
| B、x<-2 |
| C、-2<x<0或0<x<2 |
| D、-2<x<0或x>2 |
在边长为正整数的△ABC中,AB=AC,且AB边上的中线CD将△ABC的周长分为1:2的两部分,则△ABC面积的最小值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,已知∠AOB=45°,A1、A2、A3、…在射线OA上,B1、B2、B3、…在射线OB上,且A1B1⊥OA,A2B1⊥OA,…AnBn⊥OA; A2B2⊥OB,…,An+1Bn⊥OB(n=1,2,3,4,5,6…).若OA1=1,则AnBn的长是( )
如图,已知∠AOB=45°,A1、A2、A3、…在射线OA上,B1、B2、B3、…在射线OB上,且A1B1⊥OA,A2B1⊥OA,…AnBn⊥OA; A2B2⊥OB,…,An+1Bn⊥OB(n=1,2,3,4,5,6…).若OA1=1,则AnBn的长是( )A、
| ||
B、(
| ||
| C、2n | ||
| D、2n-1 |
 在某次活动课中,甲、乙两个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息:如图1,甲组测得一根直立于平地,长为80cm的竹竿的影长为60cm.如图2,乙组测得学校旗杆的影长为900cm.则旗杆的长为( )
在某次活动课中,甲、乙两个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息:如图1,甲组测得一根直立于平地,长为80cm的竹竿的影长为60cm.如图2,乙组测得学校旗杆的影长为900cm.则旗杆的长为( )| A、900cm | B、1000cm | C、1100cm | D、1200cm |
 如图,△ABC中,AB=AC,AD平分∠BAC,DE∥AC交AB于E,则S△EBD:S△ABC=( )
如图,△ABC中,AB=AC,AD平分∠BAC,DE∥AC交AB于E,则S△EBD:S△ABC=( )| A、1:2 | B、1:4 | C、1:3 | D、2:3 |
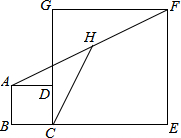 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是( )
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是( )| A、2.5 | ||||
B、
| ||||
C、
| ||||
| D、2 |

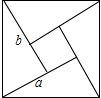 如图,我国古代数学家得出的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺构成的大正方形,若小正方形与大正方形的面积之比为1:13,则直角三角形较短的直角边a与较长的直角边b的比值为
如图,我国古代数学家得出的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺构成的大正方形,若小正方形与大正方形的面积之比为1:13,则直角三角形较短的直角边a与较长的直角边b的比值为