��Ŀ����
��ͼ����ʾ��ֱ������OABC�Ķ���A��C�ֱ���y����������x�Ḻ�����ϣ�����B��C��ֱ��l����ֱ��lƽ�ƣ�ƽ�ƺ��ֱ��l��x�ύ�ڵ�D����y�ύ�ڵ�E����1����ֱ��l����ƽ�ƣ���ƽ�ƾ���CDΪt��t��0����ֱ������OABC��ֱ��lɨ���������ͼ����Ӱ���֣�Ϊs��s����t�ĺ���ͼ����ͼ����ʾ��OMΪ�߶Σ�MNΪ�����ߵ�һ���֣�NQΪ���ߣ���NQƽ����x�ᣬN�������Ϊ4���������ϵ�AB�ij���ֱ������OABC�������
��2����2��t��4ʱ����S����t�ĺ�������ʽ��
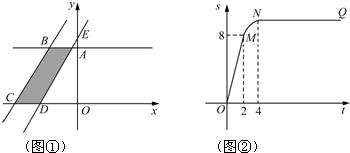
��������1���������ͼ�ο�֪M������Ϊ��2��8�����Ӷ���AB=2��OA=4����N�ĺ�����Ϊ4�����ɵ�ֱ�����ε������
��2����2��t��4ʱ����Ӱ���ֵ����=ֱ������OABC�����-������ODE�������ֻҪ��������ε�������ɣ���OD��OE�ú�t��ʽ�ӱ�ʾ���������ɵõ������ε�������ɵڣ�1���������ֱ�����ε����������Ӷ��õ���Ӱ���ֵ������
��2����2��t��4ʱ����Ӱ���ֵ����=ֱ������OABC�����-������ODE�������ֻҪ��������ε�������ɣ���OD��OE�ú�t��ʽ�ӱ�ʾ���������ɵõ������ε�������ɵڣ�1���������ֱ�����ε����������Ӷ��õ���Ӱ���ֵ������
����⣺
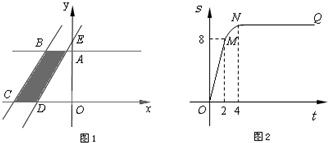
��ͼ��2��֪��M��������ǣ�2��8��
���ɴ��жϣ�AB=2��OA=4����1�֣�
��N��ĺ�������4��NQ��ƽ����x������ߣ�
��CO=4����2�֣�
��ֱ������OABC�����Ϊ��
(AB+OC)•OA=
(2+4)��4=12����3�֣�
��2����2��t��4ʱ��
��Ӱ���ֵ����=ֱ������OABC�����-������ODE�����
��S=12-
OD•OE
�ߡ�EDO=��BCO��
��tan��EDO=
=tan��BCD=
=
=2��
��OD=4-t��
��OE=2��4-t������4�֣�
��S=12-
��2��4-t��•��4-t��=12-��4-t��2
S=-t2+8t-4����5�֣�

��ͼ��2��֪��M��������ǣ�2��8��
���ɴ��жϣ�AB=2��OA=4����1�֣�
��N��ĺ�������4��NQ��ƽ����x������ߣ�
��CO=4����2�֣�
��ֱ������OABC�����Ϊ��
| 1 |
| 2 |
| 1 |
| 2 |
��2����2��t��4ʱ��
��Ӱ���ֵ����=ֱ������OABC�����-������ODE�����
��S=12-
| 1 |
| 2 |
�ߡ�EDO=��BCO��
��tan��EDO=
| OE |
| OD |
| OA |
| OC-AB |
| 4 |
| 4-2 |
��OD=4-t��
��OE=2��4-t������4�֣�
��S=12-
| 1 |
| 2 |
S=-t2+8t-4����5�֣�
������������Ҫ����ѧ�����Ķ������������������ֱ�����Ρ���������������κ�����֪ʶ����������һ���е��Ѷȵ��ۺ��⣮

��ϰ��ϵ�д�
�����Ŀ




