题目内容
从同一副扑克牌中拿出黑桃2,3,4,5,背面朝上洗匀后摆在桌面上,从中随机抽取一张(不放回),再从剩下的3张中随机抽取第二张.(1)用树状图的方法,列出前后两次抽得的扑克牌上所标数字的所有可能情况;
(2)计算抽得的两张扑克牌上数字之积为奇数的概率.
分析:(1)列举出2次放回实验的所有情况即可;
(2)看抽得的两张扑克牌上数字之积为奇数的情况占所有情况的多少即可.
(2)看抽得的两张扑克牌上数字之积为奇数的情况占所有情况的多少即可.
解答:(1)
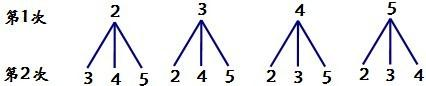
(2)解:共有12种情况,抽得的两张扑克牌上数字之积为奇数的情况有2种,P(抽得的两张扑克牌上数字之积为奇数)=
.

(2)解:共有12种情况,抽得的两张扑克牌上数字之积为奇数的情况有2种,P(抽得的两张扑克牌上数字之积为奇数)=
| 1 |
| 6 |
点评:不放回实验需注意在第一次实验只出现的数字在第二次实验中不再出现;如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
.
| m |
| n |

练习册系列答案
相关题目
 前后两次抽得的扑克
前后两次抽得的扑克 牌上所标数字的所有可能情况;
牌上所标数字的所有可能情况;