题目内容
如图,已知在Rt△ABC中,∠ABC=90°,将Rt△ABC绕点C顺时针方向旋转60°得到△DEC,点E在AC上,再将Rt△ABC沿着AB所在直线翻转180°得到△ABF,连结AD.
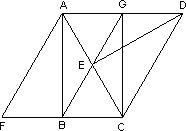
(1)求证:四边形AFCD是菱形;
(2)连结BE并延长交AD于点G,连结CG.请判断四边形ABCG是什么特殊平行四边形?证明你的结论.
答案:
解析:
解析:
|
证明:(1)∵Rt△DEC是由Rt△ABC绕点C顺时针方向旋转60°得到的, ∴AC=DC,∠ACD=60°, 1分 ∴△ACD是等边三角形,∴AD=AC=DC, 2分 ∵Rt△ABF是由Rt△ABC沿着AB所在直线翻转180°得到的, ∴AC=AF,∠ABC=∠ABF=90°, 3分 ∴∠FBC是平角,∴F、B、C三点共线, 4分 又∵∠ACB=∠ACD=60° ∴△ACF是等边三角形,∴AC=AF=CF, 5分 ∴AC=CF=DC=AD,∴四边形AFCD是菱形. 6分 (2)∵△ACD是等边三角形,DE⊥AC,∴AE=CE, 7分 ∵AD∥FC,∴∠EAG=∠ECB,∠AGE=∠CBE, 8分 ∴△AGE≌△CBE, 9分 ∴AG=CB, 10分 ∴四边形ABCG是平行四边形, 11分 ∵∠ABC=90°,∴四边形ABCG是矩形. 12分
|

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
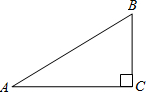 如图,已知在Rt△ABC中,∠C=90°,BC=1,AC=2,则tanA的值为( )
如图,已知在Rt△ABC中,∠C=90°,BC=1,AC=2,则tanA的值为( )| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|

 (2012•驿城区模拟)如图,已知在Rt△ABC中,∠B=90°,D、E分别是边AB、AC的中点,若DE=4,AC=10,则AB的值为( )
(2012•驿城区模拟)如图,已知在Rt△ABC中,∠B=90°,D、E分别是边AB、AC的中点,若DE=4,AC=10,则AB的值为( ) 如图,已知在Rt△ABC中,∠C=90°,内切圆的半径为3cm,外接圆的半径为12.5cm,求△ABC的三边长.
如图,已知在Rt△ABC中,∠C=90°,内切圆的半径为3cm,外接圆的半径为12.5cm,求△ABC的三边长. 如图,已知在Rt△ABC中,∠C=90°,点D在BC上,AD=BD,sin∠ADC=
如图,已知在Rt△ABC中,∠C=90°,点D在BC上,AD=BD,sin∠ADC= 如图,已知在Rt△ABC中,∠C=90°.根据要求用尺规作图:
如图,已知在Rt△ABC中,∠C=90°.根据要求用尺规作图: