题目内容
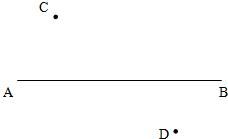
(1)根据下列语句,画出如图a图形:已知四点A、B、C、D.
①画直线AB;
②连接AC、BD,相交于点O;
③画射线AD、BC,交于点P.
(2)一个角的余角比它的补角的
还少20°,求这个角的大小.
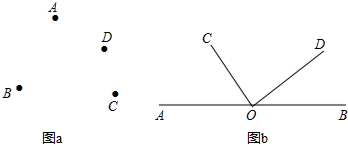
(3)如图b,AOB为直线,OC平分∠AOD,∠BOD=42°,求∠AOC的度数.
①画直线AB;
②连接AC、BD,相交于点O;
③画射线AD、BC,交于点P.
(2)一个角的余角比它的补角的
| 1 | 3 |
(3)如图b,AOB为直线,OC平分∠AOD,∠BOD=42°,求∠AOC的度数.

分析:(1)根据直线、射线、线段的性质画图即可;
(2)首先根据余角与补角的定义,设这个角为x,则它的余角为(90°-x),补角为(180°-x),再根据题中给出的等量关系列方程即可求解.
(3)根据题意找出这几个角之间的关系,利用角平分线的性质来求.
(2)首先根据余角与补角的定义,设这个角为x,则它的余角为(90°-x),补角为(180°-x),再根据题中给出的等量关系列方程即可求解.
(3)根据题意找出这几个角之间的关系,利用角平分线的性质来求.
解答:解:(1)①②③如图a所示:

(2)设这个角为x,则它的余角为(90°-x),补角为(180°-x),
根据题意可,得90°-x=
(180°-x)-20°,
解得x=75°,
所以这个角为75°.
(3)∵AOB是直线,
∴∠AOD+∠BOD=180°,
∴∠AOD=180°-∠BOD=180°-42°=138°,
∵OC平分∠AOD,
∴∠AOC=
∠AOD=138°=69°,
∴∠AOC的度数为69°.

(2)设这个角为x,则它的余角为(90°-x),补角为(180°-x),
根据题意可,得90°-x=
| 1 |
| 3 |
解得x=75°,
所以这个角为75°.
(3)∵AOB是直线,
∴∠AOD+∠BOD=180°,
∴∠AOD=180°-∠BOD=180°-42°=138°,
∵OC平分∠AOD,
∴∠AOC=
| 1 |
| 2 |
∴∠AOC的度数为69°.
点评:(1)此题主要考查了复杂作图,解答此题需要熟练掌握方位角的概念,直线、射线、线段的性质,认真作图解答即可.
(2)本题考查了余角与补角的定义,解答此类题一般先用未知数表示所求角的度数,再根据一个角的余角和补角列出代数式和方程求解,难度适中.
(3)本题考查了角的有关计算,解题的关键是找出各角之间的关系,OC平分∠AOD,求出∠AOC的度数.
(2)本题考查了余角与补角的定义,解答此类题一般先用未知数表示所求角的度数,再根据一个角的余角和补角列出代数式和方程求解,难度适中.
(3)本题考查了角的有关计算,解题的关键是找出各角之间的关系,OC平分∠AOD,求出∠AOC的度数.

练习册系列答案
相关题目
 23、根据下列语句,用三角板、圆规或直尺作图,不要求写作法:
23、根据下列语句,用三角板、圆规或直尺作图,不要求写作法: