题目内容
(2008•西宁)如图,已知半径为1的⊙O1与x轴交于A,B两点,OM为⊙O1的切线,切点为M,圆心O1的坐标为(2,0),二次函数y=-x2+bx+c的图象经过A,B两点.(1)求二次函数的解析式;
(2)求切线OM的函数解析式;
(3)线段OM上存在一点P,使得以P,O,A为顶点的三角形与△OO1M相似.请问有几个符合条件的点P并分别求出它们的坐标.

【答案】分析:(1)根据圆心的坐标和半径的长即可求出A,B两点的坐标,然后将A,B的坐标代入抛物线中即可得出二次函数的解析式.
(2)可先在直角三角形OO1M中求出∠MO1O的度数,然后过M作x轴的垂线,设垂足为F,可在直角三角形MO1F中根据∠MO1O的度数和MO1的长求出MF和O1F的长,即可得出M点的坐标,进而可根据M的坐标求出直线OM的解析式.
(3)由于P在OM上,因此∠POA=∠MOO1,因此本题可分两种情况进行讨论:
①当AP∥O1M时,②当PA⊥OB时.据此可求出P点的坐标.(①可参照求M点坐标时的方法来解,②可直接将A点横坐标代入直线OM的解析式中,即可求出P的坐标).
解答:解:(1)∵圆心的坐标为O1(2,0),⊙O1半径为1,
∴A(1,0),B(3,0),
∵二次函数y=-x2+bx+c的图象经过点A,B,
∴可得方程组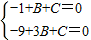 ,
,
解得: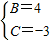 ,
,
∴二次函数解析式为y=-x2+4x-3.
(2)过点M作MF⊥X轴,垂足为F.
∵OM是⊙O1的切线,M为切点,
∴O1M⊥OM(圆的切线垂直于经过切点的半径).
在RT△OO1M中,sin∠O1OM=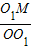 =
= ,
,
∵∠O1OM为锐角,
∴∠O1OM=30°,
∴OM=OO1•cos30°=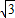 ,
,
在RT△MOF中,OF=OM•cos30°= .
.
MF=OMsin30°= .
.
∴点M坐标为(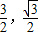 ),
),
设切线OM的函数解析式为y=kx(k≠0),由题意可知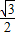 =
= k,
k,
∴k=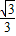 ,
,
∴切线OM的函数解析式为y= x
x
(3)两个,
①过点A作AP1⊥x轴,与OM交于点P1,
可得Rt△AP1O∽Rt△MO1O(两角对应相等两三角形相似),
P1A=OA•tan∠AOP1=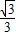 ,
,
∴P1(1,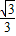 );
);
②过点A作AP2⊥OM,垂足为,过P2点作P2H⊥OA,垂足为H.
可得Rt△OP2A∽Rt△O1MO(两角对应相等两三角形相似),
在Rt△OP2A中,
∵OA=1,
∴P2=OA•cos30°=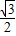 ,
,
在Rt△OP2H中,OH=OP2•cos∠AOP2= ,
,
P2H=OP2•sin∠AOP2=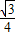 ,P2(
,P2( ,
,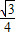 ),
),
∴符合条件的P点坐标有(1,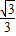 ),(
),( ,
,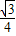 ).
).
点评:本题主要考查了切线的性质,一次函数和二次函数解析式的确定,相似三角形的判定和性质等知识点.
考查学生分类讨论,数形结合的数学思想方法.
(2)可先在直角三角形OO1M中求出∠MO1O的度数,然后过M作x轴的垂线,设垂足为F,可在直角三角形MO1F中根据∠MO1O的度数和MO1的长求出MF和O1F的长,即可得出M点的坐标,进而可根据M的坐标求出直线OM的解析式.
(3)由于P在OM上,因此∠POA=∠MOO1,因此本题可分两种情况进行讨论:
①当AP∥O1M时,②当PA⊥OB时.据此可求出P点的坐标.(①可参照求M点坐标时的方法来解,②可直接将A点横坐标代入直线OM的解析式中,即可求出P的坐标).
解答:解:(1)∵圆心的坐标为O1(2,0),⊙O1半径为1,
∴A(1,0),B(3,0),
∵二次函数y=-x2+bx+c的图象经过点A,B,
∴可得方程组
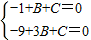 ,
,解得:
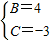 ,
,∴二次函数解析式为y=-x2+4x-3.
(2)过点M作MF⊥X轴,垂足为F.

∵OM是⊙O1的切线,M为切点,
∴O1M⊥OM(圆的切线垂直于经过切点的半径).
在RT△OO1M中,sin∠O1OM=
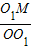 =
= ,
,∵∠O1OM为锐角,
∴∠O1OM=30°,
∴OM=OO1•cos30°=
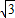 ,
,在RT△MOF中,OF=OM•cos30°=
 .
.MF=OMsin30°=
 .
.∴点M坐标为(
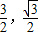 ),
),设切线OM的函数解析式为y=kx(k≠0),由题意可知
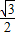 =
= k,
k,∴k=
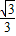 ,
,∴切线OM的函数解析式为y=
 x
x(3)两个,
①过点A作AP1⊥x轴,与OM交于点P1,
可得Rt△AP1O∽Rt△MO1O(两角对应相等两三角形相似),
P1A=OA•tan∠AOP1=
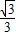 ,
,∴P1(1,
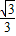 );
);②过点A作AP2⊥OM,垂足为,过P2点作P2H⊥OA,垂足为H.
可得Rt△OP2A∽Rt△O1MO(两角对应相等两三角形相似),
在Rt△OP2A中,
∵OA=1,
∴P2=OA•cos30°=
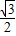 ,
,在Rt△OP2H中,OH=OP2•cos∠AOP2=
 ,
,P2H=OP2•sin∠AOP2=
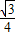 ,P2(
,P2( ,
,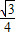 ),
),∴符合条件的P点坐标有(1,
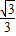 ),(
),( ,
,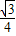 ).
).点评:本题主要考查了切线的性质,一次函数和二次函数解析式的确定,相似三角形的判定和性质等知识点.
考查学生分类讨论,数形结合的数学思想方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2008•西宁)如图,一块三角形模具的阴影部分已破损.
(2008•西宁)如图,一块三角形模具的阴影部分已破损.

