题目内容
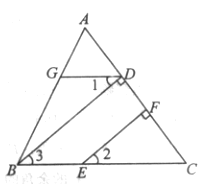
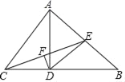
【题目】如图,AD是△ABC的高,CE是△ABC的中线.
(1)若AD=12,BD=16,求DE;
(2)已知点F是中线CE的中点,连接DF,若∠AEC=57°,∠DFE=90°,求∠BCE的度数.
【答案】(1)DE=10;(2)∠BCE=19°.
【解析】
(1)根据勾股定理和直角三角形斜边上的中线等于斜边的一半即可得到结论;
(2)由DE=DC得到∠DEC=∠DCE,由DE=BE得到∠B=∠EDB,由此根据外角的性质来求∠BCE的度数.
(1)∵AD⊥BC,
∴∠ADB=90°,
∴AB=![]() =20,
=20,
∵CE是中线,
∴DE是斜边AB上的中线,
∴DE=![]() AB=10;
AB=10;
(2)∵DF⊥CF,F是CF的中点,
∴DE=DC,
∴∠DEC=∠DCE,
∴∠EDB=∠DEC+∠DCE=2∠BCE,
∵DE=BE,
∴∠B=∠EDB,
∴∠B=2∠BCE,
∴∠AEC=3∠BCE=57°,则∠BCE=19°.

练习册系列答案
相关题目