题目内容
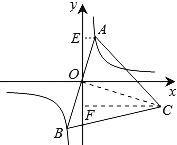
【题目】如图,已知点A是双曲线![]() 在第三象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线
在第三象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线![]() 上运动,则k的值是 .
上运动,则k的值是 .

【答案】﹣3![]()
【解析】试题分析:根据反比例函数的性质得出OA=OB,连接OC,过点A作AE⊥y轴,垂足为E,过点C作CF⊥y轴,垂足为F,根据等边三角形的性质和解直角三角形求出OC=![]() OA,求出△OFC∽△AEO,相似比
OA,求出△OFC∽△AEO,相似比![]() ,求出面积比
,求出面积比 ,求出△OFC的面积,即可得出答案.∵双曲线
,求出△OFC的面积,即可得出答案.∵双曲线![]() 的图象关于原点对称,
的图象关于原点对称,
∴点A与点B关于原点对称, ∴OA=OB, 连接OC,如图所示, ∵△ABC是等边三角形,OA=OB,
∴OC⊥AB.∠BAC=60°, ∴tan∠OAC=![]() =
=![]() , ∴OC=
, ∴OC=![]() OA,
OA,
过点A作AE⊥y轴,垂足为E,过点C作CF⊥y轴,垂足为F, ∵AE⊥OE,CF⊥OF,OC⊥OA,
∴∠AEO=∠OFC,∠AOE=90°﹣∠FOC=∠OCF, ∴△OFC∽△AEO,相似比![]() , ∴面积比
, ∴面积比 ,
,
∵点A在第一象限,设点A坐标为(a,b), ∵点A在双曲线![]() 上, ∴S△AEO=
上, ∴S△AEO=![]() ab=
ab=![]() ,
,
∴S△OFC=![]() FCOF=
FCOF=![]() , ∴设点C坐标为(x,y), ∵点C在双曲线
, ∴设点C坐标为(x,y), ∵点C在双曲线![]() 上, ∴k=xy,
上, ∴k=xy,
∵点C在第四象限, ∴FC=x,OF=﹣y. ∴FCOF=x(﹣y)=﹣xy=﹣![]()

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
