题目内容
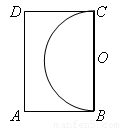
如图，王大伯家屋后有一块长12m，宽8m的矩形空地，他在以长边BC为直径的半圆内种菜，他家养的一只羊平时拴A处的一棵树上，为了不让羊吃到菜，拴羊的绳长可以选用（ ）| A、3m | B、5m | C、7m | D、9m |
分析：为了不让羊吃到菜，必须＜等于点A到圆的最小距离．要确定最小距离，连接OA交半圆于点E，即AE是最短距离．在直角三角形AOB中，因为OB=6，AB=8，所以根据勾股定理得OA=10．那么AE的长即可解答．
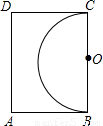
解答：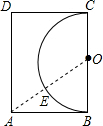
解：连接OA，交半圆O于E点，
在Rt△OAB中，OB=6，AB=8，
所以OA=
=10；
又OE=OB=6，
所以AE=OA-OE=4．
因此选用的绳子应该不大于4m，
故选A．
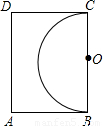
解：连接OA，交半圆O于E点，在Rt△OAB中，OB=6，AB=8，
所以OA=
| OB2+AB2 |
又OE=OB=6，
所以AE=OA-OE=4．
因此选用的绳子应该不大于4m，
故选A．
点评：此题确定点到半圆的最短距离是难点．熟练运用勾股定理．
练习册系列答案
相关题目
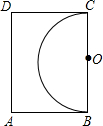
如图，王大伯家屋后有一块长12m，宽8m的矩形空地，他在以长边BC为直径的半圆内种菜，他家养的一只羊平时拴在A处的一棵树上，为了不让羊吃到菜，拴羊的绳长应不超过
为直径的半圆内种菜，他家养的一只羊平时拴在
处的一棵树上，为了不让羊吃到菜，拴羊的绳长可以选用（ ）
