题目内容
已知反比例函数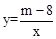 (m为常数)的图象经过点A(-1,6).
(m为常数)的图象经过点A(-1,6).
(1)求m的值;
(2)如图,过点A作直线AC与函数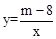 的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标.
的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标.
(1)2;(2)(﹣4,0).
解析试题分析:(1)将A点坐标代入反比例函数解析式即可得到一个关于m的一元一次方程,求出m的值;
(2)分别过点A、B作x轴的垂线,垂足分别为点E、D,则△CBD∽△CAE,运用相似三角形知识求出CD的长即可求出点C的横坐标.
试题解析:(1)∵图象过点A(﹣1,6),∴ =6,解得m=2.
=6,解得m=2.
(2)如图,分别过点A、B作x轴的垂线,垂足分别为点E、D,
由题意得,AE=6,OE=1,即A(﹣1,6).
∵BD⊥x轴,AE⊥x轴,∴AE∥BD.
∴△CBD∽△CAE. ∴ .
.
∵AB=2BC,∴ ,即
,即 .
.
∴BD=2,即点B的纵坐标为2.
当y=2时,x=-3,即B(-3,2).
设直线AB方程为:y=kx+b,
把A和B坐标代入得: ,解得
,解得 .
.
∴直线AB为y=2x+8.
令y=0,解得x=﹣4,∴C(﹣4,0).
考点:1.反比例函数综合题;2.待定系数法;3.曲线上点的坐标与方程的关系;4.相似三角形的判定和性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的图象经过点(﹣2,3),则k的值为 .
的图象经过点(﹣2,3),则k的值为 . 的图象上.
的图象上.
 的图象相交于A(-1,4)、B(4,-1)两点,直线l⊥x轴于点E(-4,0),与反比例函数和一次函数的图象分别相交于点C、D,连接AC、BC
的图象相交于A(-1,4)、B(4,-1)两点,直线l⊥x轴于点E(-4,0),与反比例函数和一次函数的图象分别相交于点C、D,连接AC、BC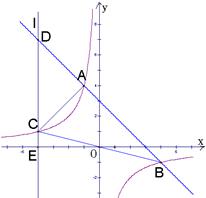
 ,若存在,请求出P的坐标,若不存在,请说明理由。
,若存在,请求出P的坐标,若不存在,请说明理由。 与反比例函数
与反比例函数 的图象相交于点A(-1,a),并且与x轴相交于点B.
的图象相交于点A(-1,a),并且与x轴相交于点B.
 的图象与反比例函数
的图象与反比例函数 (
( )的图象相交于A、B两点,点A的纵坐标为2.(1)求反比例函数的解析式;(2)求出点B的坐标,并根据函数图象,写出当y1>y2时,自变量
)的图象相交于A、B两点,点A的纵坐标为2.(1)求反比例函数的解析式;(2)求出点B的坐标,并根据函数图象,写出当y1>y2时,自变量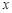 的取值范围.
的取值范围.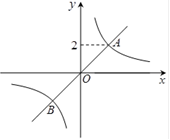
 的图象与反比例函数
的图象与反比例函数 的图象在第一象限内交于点
的图象在第一象限内交于点 ,与
,与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 ,
, 。
。
 ,使得
,使得 ,求点
,求点 (x>0)的图象交于 A(a,1)、B(1,b)两点.
(x>0)的图象交于 A(a,1)、B(1,b)两点.
 (k>0,x>0)与OA边交于点E,过点F作FC⊥x轴于点C,连结EF、OF.
(k>0,x>0)与OA边交于点E,过点F作FC⊥x轴于点C,连结EF、OF.
 ,求反比例函数的解析式;
,求反比例函数的解析式;