题目内容
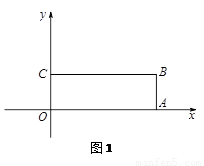
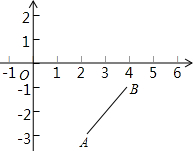
如图,已知平面直角坐标系,A、B两点的坐标分别为A(2,-3),B(4,-1).(1)若P(p,0)是x轴上的一个动点,则当p=
(2)若C(a,0),D(a+3,0)是x轴上的两个动点,则当a=
(3)设M,N分别为x轴和y轴上的动点,请问:是否存在这样的点M(m,0)、N(0,n),使四边形
 ABMN的周长最短?若存在,请求出m=
ABMN的周长最短?若存在,请求出m=分析:(1)根据题意,设出并找到B(4,-1)关于x轴的对称点是B',其坐标为(4,1),进而可得直线AB'的解析式,进而可得答案;
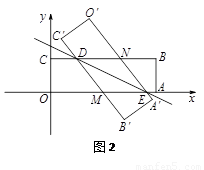
(2)过A点作AE⊥x轴于点E,且延长AE,取A'E=AE.做点F(1,-1),连接A'F.利用两点间的线段最短,可知四边形ABDC的周长最短等于A'F+CD+AB,从而确定C点的坐标值.
(3)根据对称轴的性质,可得存在使四边形ABMN周长最短的点M、N,当且仅当m=
,n=-
;时成立.
(2)过A点作AE⊥x轴于点E,且延长AE,取A'E=AE.做点F(1,-1),连接A'F.利用两点间的线段最短,可知四边形ABDC的周长最短等于A'F+CD+AB,从而确定C点的坐标值.
(3)根据对称轴的性质,可得存在使四边形ABMN周长最短的点M、N,当且仅当m=
| 5 |
| 2 |
| 5 |
| 3 |
解答: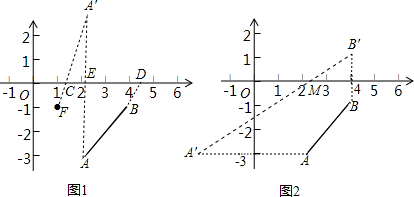 解:(1)设点B(4,-1)关于x轴的对称点是B',其坐标为(4,1),
解:(1)设点B(4,-1)关于x轴的对称点是B',其坐标为(4,1),
设直线AB'的解析式为y=kx+b,
把A(2,-3),B'(4,1)代入得:
,
解得
,
∴y=2x-7,
令y=0得x=
,
即p=
.
(2)过A点作AE⊥x轴于点E,且延长AE,取A'E=AE.做点F(1,-1),连接A'F.那么A'(2,3).
直线A'F的解析式为y-1=
•(x-1),即y=4x-5,
∵C点的坐标为(a,0),且在直线A'F上,
∴a=
.
(3)存在使四边形ABMN周长最短的点M、N,
作A关于y轴的对称点A′,作B关于x轴的对称点B′,连接A′B′,与x轴、y轴的交点即为点M、N,
∴A′(-2,-3),B′(4,1),
∴直线A′B′的解析式为:y=
x-
,
∴M(
,0),N(0,-
).
m=
,n=-
.
 解:(1)设点B(4,-1)关于x轴的对称点是B',其坐标为(4,1),
解:(1)设点B(4,-1)关于x轴的对称点是B',其坐标为(4,1),设直线AB'的解析式为y=kx+b,
把A(2,-3),B'(4,1)代入得:
|
解得
|
∴y=2x-7,
令y=0得x=
| 7 |
| 2 |
即p=
| 7 |
| 2 |
(2)过A点作AE⊥x轴于点E,且延长AE,取A'E=AE.做点F(1,-1),连接A'F.那么A'(2,3).
直线A'F的解析式为y-1=
| 3-(-1) |
| 2-1 |
∵C点的坐标为(a,0),且在直线A'F上,
∴a=
| 5 |
| 4 |
(3)存在使四边形ABMN周长最短的点M、N,
作A关于y轴的对称点A′,作B关于x轴的对称点B′,连接A′B′,与x轴、y轴的交点即为点M、N,
∴A′(-2,-3),B′(4,1),
∴直线A′B′的解析式为:y=
| 2 |
| 3 |
| 5 |
| 3 |
∴M(
| 5 |
| 2 |
| 5 |
| 3 |
m=
| 5 |
| 2 |
| 5 |
| 3 |
点评:考查图形的轴对称在实际中的运用,同时考查了根据两点坐标求直线解析式,运用解析式求直线与坐标轴的交点等知识.

练习册系列答案
相关题目
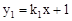 的图象与y轴交于点A,
的图象与y轴交于点A,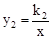 的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐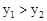 时x的取值范围。
时x的取值范围。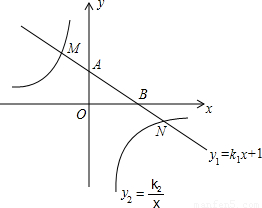
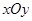 中,四边形OABC是矩形,点A,C的坐
中,四边形OABC是矩形,点A,C的坐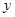 =-
=-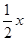 +
+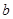 交折线O-A-B于点E.
交折线O-A-B于点E.