题目内容
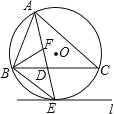
【题目】如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.
(1)判断直线l与⊙O的位置关系,并说明理由;
(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;
(3)在(2)的条件下,若DE=4,DF=3,求AF的长.
【答案】(1)直线l与⊙O相切.理由详见解析;(2)证明详见解析;(3)![]() .
.
【解析】
试题分析:(1)连接OE、OB、OC.由题意可证明![]() ,于是得到∠BOE=∠COE,由等腰三角形三线合一的性质可证明OE⊥BC,于是可证明OE⊥l,故此可证明直线l与⊙O相切;
,于是得到∠BOE=∠COE,由等腰三角形三线合一的性质可证明OE⊥BC,于是可证明OE⊥l,故此可证明直线l与⊙O相切;
(2)先由角平分线的定义可知∠ABF=∠CBF,然后再证明∠CBE=∠BAF,于是可得到∠EBF=∠EFB,最后依据等角对等边证明BE=EF即可;
(3)先求得BE的长,然后证明△BED∽△AEB,由相似三角形的性质可求得AE的长,于是可得到AF的长.
试题解析:(1)直线l与⊙O相切.理由如下:
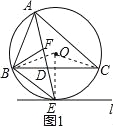
如图1所示:连接OE、OB、OC.
∵AE平分∠BAC,
∴∠BAE=∠CAE.
∴![]() .
.
∴∠BOE=∠COE.
又∵OB=OC,
∴OE⊥BC.
∵l∥BC,
∴OE⊥l.
∴直线l与⊙O相切.
(2)∵BF平分∠ABC,
∴∠ABF=∠CBF.
又∵∠CBE=∠CAE=∠BAE,
∴∠CBE+∠CBF=∠BAE+∠ABF.
又∵∠EFB=∠BAE+∠ABF,
∴∠EBF=∠EFB.
∴BE=EF.
(3)由(2)得BE=EF=DE+DF=7.
∵∠DBE=∠BAE,∠DEB=∠BEA,
∴△BED∽△AEB.
∴![]() ,即
,即![]() ,解得;AE=
,解得;AE=![]() ,
,
∴AF=AE﹣EF=![]() ﹣7=
﹣7=![]() .
.

【题目】根据国家卫健委统计数据,目前我国健康素养水平中,城市、农村居民水平分别约为25%,15%,东部中部和西部地区居民水平分别约为24%、16%、14%.这些数据的中位数是____________.
【题目】老师对某班全体学生在电脑培训前后进行了一次水平测试,考分以同一标准划分为“不合格”、“合格”、“优秀”三个等级,成绩见下表.下列说法错误的是( )
成绩 | 培训前 | 培训后 |
不合格 | 40 | 10 |
合格 | 8 | 25 |
优秀 | 2 | 15 |
A.培训前“不合格”的学生占80%
B.培训前成绩“合格”的学生是“优秀”学生的4倍
C.培训后80%的学生成绩达到了“合格”以上
D.培训后优秀率提高了30%