Question

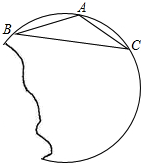如图所示，要把破残的圆片复制完整．已知弧上的三点A、B、C．
（1）用尺规作图法找出

BAC

所在圆的圆心．（保留作图痕迹，不写作法）
（2）设△ABC是等腰三角形，底边BC=8cm，腰AB=5cm．求圆片的半径R．

Answer 1

分析：（1）作图思路：可根据AB，AC的垂直平分线来确定圆心．
（2）本题可通过构建直角三角形来求解．连接AO交BC于E．先求出AE的值，然后在直角三角形OBE中，用半径表示出OE，OB，然后根据勾股定理求出半径的值．

解答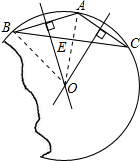：解：（1）分别作AB、AC的垂直平分线，设交点为O
则O为所求圆的圆心

（2）连接AO交BC于E，∵AB=AC
∴AE⊥BC，BE=

1

2

BC=4
在Rt△ABE中，AE=

AB2-BE2

=

52-42

=3
设⊙O的半径为R，在Rt△BEO中
OB²=BE²+OE²，即R²=4²+（R-3）²
∴R²=16+R²-6R+9
∴R=

25

6

（cm）
所以所求圆的半径为

25

6

cm．

点评：本题综合考查了垂径定理，勾股定理等知识点，要注意作图中是根据垂径定理作为作图依据的．