题目内容
已知:如图,三个半圆依次相外切,它们的圆心都在x轴的正半轴上并与直线y= x相切,设
x相切,设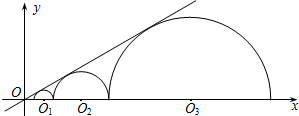 半圆C1、半圆C2、半圆C3的半径分别是r1、r2、r3,则当r1=1时,r3=________.
半圆C1、半圆C2、半圆C3的半径分别是r1、r2、r3,则当r1=1时,r3=________.
9
分析:分别过O1、O2、O3作直线y= x的垂线,垂足为A、B、C,再分别过O1、O2作O1D⊥O2B,O2E⊥O3C,垂足为D、E,由直线解析式可知∠COO3=∠DO1O2=∠EO2O3=30°,分别解Rt△DO1O2,Rt△EO2O3,求r3.
x的垂线,垂足为A、B、C,再分别过O1、O2作O1D⊥O2B,O2E⊥O3C,垂足为D、E,由直线解析式可知∠COO3=∠DO1O2=∠EO2O3=30°,分别解Rt△DO1O2,Rt△EO2O3,求r3.
解答: 解:如图,过O1、O2、O3作直线的垂线,垂足为A、B、C,
解:如图,过O1、O2、O3作直线的垂线,垂足为A、B、C,
过O1、O2作O1D⊥O2B,O2E⊥O3C,垂足为D、E,
∵直线解析式为y= x,
x,
∴∠COO3=∠DO1O2=∠EO2O3=30°,
在Rt△DO1O2中,O1O2=r1+r2,O2D=r2-r1,由sin∠DO1O2= ,得
,得 =
=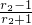 ,解得r2=3;
,解得r2=3;
在Rt△EO2O3中,O2O3=r2+r3,O3E=r3-r2,由sin∠EO2O3= ,得
,得 =
= ,解得r3=9.
,解得r3=9.
故答案为:9.
点评:本题考查了一次函数的综合运用.关键是根据一次函数解析式求出直线与x轴的夹角,把问题转化到直角三角形中求解.
分析:分别过O1、O2、O3作直线y=
 x的垂线,垂足为A、B、C,再分别过O1、O2作O1D⊥O2B,O2E⊥O3C,垂足为D、E,由直线解析式可知∠COO3=∠DO1O2=∠EO2O3=30°,分别解Rt△DO1O2,Rt△EO2O3,求r3.
x的垂线,垂足为A、B、C,再分别过O1、O2作O1D⊥O2B,O2E⊥O3C,垂足为D、E,由直线解析式可知∠COO3=∠DO1O2=∠EO2O3=30°,分别解Rt△DO1O2,Rt△EO2O3,求r3.解答:
 解:如图,过O1、O2、O3作直线的垂线,垂足为A、B、C,
解:如图,过O1、O2、O3作直线的垂线,垂足为A、B、C,过O1、O2作O1D⊥O2B,O2E⊥O3C,垂足为D、E,
∵直线解析式为y=
 x,
x,∴∠COO3=∠DO1O2=∠EO2O3=30°,
在Rt△DO1O2中,O1O2=r1+r2,O2D=r2-r1,由sin∠DO1O2=
 ,得
,得 =
=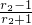 ,解得r2=3;
,解得r2=3;在Rt△EO2O3中,O2O3=r2+r3,O3E=r3-r2,由sin∠EO2O3=
 ,得
,得 =
= ,解得r3=9.
,解得r3=9.故答案为:9.
点评:本题考查了一次函数的综合运用.关键是根据一次函数解析式求出直线与x轴的夹角,把问题转化到直角三角形中求解.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案
相关题目
 半圆C1、半圆C2、半圆C3的半径分别是r1、r2、r3,则当r1=1时,r3=
半圆C1、半圆C2、半圆C3的半径分别是r1、r2、r3,则当r1=1时,r3= 已知:如图,三个半圆彼此相外切,它们的圆心都在x轴的正半轴上并与直线y=
已知:如图,三个半圆彼此相外切,它们的圆心都在x轴的正半轴上并与直线y= 已知:如图,三个半圆彼此相外切,它们的圆心都在x轴的正半轴上并与直线y=
已知:如图,三个半圆彼此相外切,它们的圆心都在x轴的正半轴上并与直线y=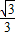 x相切,设半圆C1、半圆C2、半圆C3的半径分别是r1、r2、r3,则当r1=1时,r3= .
x相切,设半圆C1、半圆C2、半圆C3的半径分别是r1、r2、r3,则当r1=1时,r3= .