题目内容
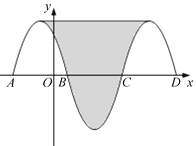
【题目】已知二次函数y=x2-2m x+m2+m+1的图像与x轴交于A、B两点,点C为顶点.
(1)求m的取值范围;
(2)若将二次函数的图像关于x轴翻折,所得图像的顶点为D,若CD=8.求四边形ACBD的面积。
【答案】(1)m<-1(2)16.
【解析】试题分析:(1)根据判别式的意义得到△=4m2-4(m2+m+1)=-4m-4>0,然后解不等式即可;
(2)先配方得到y=(x-m)2+m+1,则顶点的纵坐标为m+1,利用C点和D点关于x轴对称得到m+1=-4,解得m=-5,所以y=x2+10x+21,然后解方程x2+10x+21=0得到A(-3,0),B(-7,0),再利用三角形面积公式计算四边形ACBD的面积.
试题解析:(1)∵二次函数图象与x轴有两个交点,
∴△=4m2-4(m2+m+1)=-4m-4>0,
∴m<-1;
(2)y=x2-2mx+m2+m+1=(x-m)2+m+1,
∵CD=8,
∴m+1=-4,解得m=-5,
∴y=x2+10x+21,
令y=0,x2+10x+21=0,解得x1=-3,x2=-7,则A(-3,0),B(-7,0)
∴AB=4,
∴S四边形ACBD=2×![]() ×4×4=16.
×4×4=16.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目