ЬтФПФкШн
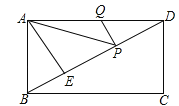
ЁОЬтФПЁПдкЁїABCжаЃЌЁЯBACЃН90ЁуЃЌABЃНACЕуDЮЊжБЯпBCЩЯвЛЖЏЕу(ЕуDВЛгыBЁЂCжиКЯ) ЃЎвдADЮЊБпзїе§ЗНаЮADEFЃЌСЌНгCFЃЎ
ЃЈ1ЃЉШчЭМЂйЃЌЕБЕуDдкЯпЖЮBCЩЯЪБЃЌЧѓжЄЃКЂйBDЁЭCFЃЛЂкCFЃНBCCDЃЎ
ЃЈ2ЃЉШчЭМЂкЃЌЕБЕуDдкЯпЖЮBCЕФбгГЄЯпЩЯЪБЃЌЦфЫћЬѕМўВЛБфЃЌЧыжБНгаДГіCFЁЂBCЁЂCDШ§ЬѕЯпЖЮжЎМфЕФЙиЯЕЃЎ
ЃЈ3ЃЉШчЭМЂлЃЌЕБЕуDдкЯпЖЮBCЕФЗДЯђбгГЄЯпЩЯЪБЃЌЧвЕуAЁЂFЗжБ№дкжБЯпBCЕФСНВрЃЌЦфЫћЬѕМўВЛБфЃКЂйЧыжБНгаДГіCFЁЂBCЁЂCDШ§ЬѕЯпЖЮжЎМфЕФЙиЯЕЃЛЂкШєСЌНге§ЗНаЮЖдНЧЯпAEЁЂDF,НЛЕуЮЊOЃЌСЌНгOCЃЌЬНОПЁїAOCЕФаЮзДЃЌВЂЫЕУїРэгЩЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉ
жЄУїЃКЂйШчЭМЂйЃЌ
ЁпЁЯBAC=90ЁуЃЌAB=ACЃЌ
ЁрЁЯACB=ЁЯABC=45ЁуЃЌ
ЁпЫФБпаЮADEFЪЧе§ЗНаЮЃЌ
ЁрAD=AFЃЌЁЯDAF=90ЁуЃЌ
ЁпЁЯBAD=90Ёу-ЁЯDACЃЌЁЯCAF=90Ёу-ЁЯDACЃЌ
ЁрЁЯBAD=ЁЯCAFЃЌ
дкЁїBADКЭЁїCAFжаЃЌ
|
ЁрЁїBADЁеЁїCAFЃЈSASЃЉЃЌ
ЁрЁЯACF=ЁЯABD=45ЁуЃЌ
ЁрЁЯBCF=90ЁуЃЌ
МДBDЁЭCF.
ЂкгЩЂйЕУЁїBADЁеЁїCAFЃЌ
ЁрBD=CF
ЁпBD+CD=BCЃЌ
ЁрCF=BC-CD.
ЃЛ
ЃЛ
ЃЛ
ЃЛ
ЃЛ
ЃЛ
ЃЈ2ЃЉ
НтЃКCF-CD=BCЃЎРэгЩШчЯТЃК
ШчЭМЂкЃЌ
ЁпЁЯBAD=90Ёу+ЁЯCADЃЌ
ЁЯCAF=90Ёу+ЁЯCADЃЌ
ЁрЁЯBAD=ЁЯCAFЃЌ
дкЁїBADКЭЁїCAFжаЃЌ
|
ЁрЁїBADЁеЁїCAFЃЈSASЃЉЃЌ
ЁрBD=CFЃЌ
ЁпBD=BC+CDЃЌ
ЁрCF-CD=BCЃЎ
ЃЛ
ЃЛ
ЃЛ
ЃЛ
ЃЛ
ЃЛ
ЃЈ3ЃЉ
НтЃКЂйCD-CF=BC;
ЂкЕШбќШ§НЧаЮ.РэгЩШчЯТЃК
ЁпЁЯBAC=90ЁуЃЌЁЯABC=45ЁуЃЌ
ЁрЁЯACB=ЁЯABC=45ЁуЃЌ
ЁрAB=ACЃЌ
ЁпЫФБпаЮADEFЪЧе§ЗНаЮЃЌ
ЁрAD=AFЃЌЁЯDAF=90ЁуЃЌ
ЁпЁЯBAD=90Ёу-ЁЯBAFЃЌЁЯCAF=90Ёу-ЁЯBAFЃЌ
ЁрЁЯBAD=ЁЯCAFЃЌ
ЁпдкЁїBADКЭЁїCAFжаЃЌ
|
ЁрЁїBADЁеЁїCAFЃЈSASЃЉЃЌ
ЁрЁЯACF=ЁЯABDЃЌ
ЁпЁЯABC=45ЁуЃЌ
ЁрЁЯABD=135ЁуЃЌ
ЁрЁЯACF=ЁЯABD=135ЁуЃЌ
ЁрЁЯFCD=90ЁуЃЌ
ЁрЁїFCDЪЧжБНЧШ§НЧаЮЃЎ
гжЁпOD=OFЃЌ
ЁрOC=OD=OAЃЌ
ЁрЁїAOCЪЧЕШбќШ§НЧаЮ.
ЃЛ
ЃЛ
ЃЛ
ЃЛ
ЃЛ
ЃЛ
ЁОНтЮіЁПЃЈ1ЃЉЃЌЃЈ2ЃЉКЭЃЈ3ЃЉжаУПЬтЖМвЊдЫгУЁАSASЁБжЄУїЁїBADЁеЁїCAFЃЌШЛКѓЕУЕНБпЕФЙиЯЕКЭНЧЕФЙиЯЕЃЛЃЈ3ЃЉЕФЂкЛЙвЊдЫгУЕНжБНЧШ§НЧаЮжааББпЩЯЕФжаЯпЪЧаББпГЄЕФвЛАы.
ЁОПМЕуОЋЮіЁПРћгУЕШбќжБНЧШ§НЧаЮКЭжБНЧШ§НЧаЮаББпЩЯЕФжаЯпЖдЬтФПНјааХаЖЯМДПЩЕУЕНД№АИЃЌашвЊЪьжЊЕШбќжБНЧШ§НЧаЮЪЧСНЬѕжБНЧБпЯрЕШЕФжБНЧШ§НЧаЮЃЛЕШбќжБНЧШ§НЧаЮЕФСНИіЕзНЧЯрЕШЧвЕШгк45ЁуЃЛжБНЧШ§НЧаЮаББпЩЯЕФжаЯпЕШгкаББпЕФвЛАыЃЎ

 ПЮГЬДяБъВтЪдОэДГЙи100ЗжЯЕСаД№АИ
ПЮГЬДяБъВтЪдОэДГЙи100ЗжЯЕСаД№АИ аТОэЭѕЦкФЉГхДЬ100ЗжЯЕСаД№АИ
аТОэЭѕЦкФЉГхДЬ100ЗжЯЕСаД№АИ ШЋФмДГЙи100ЗжЯЕСаД№АИ
ШЋФмДГЙи100ЗжЯЕСаД№АИ