题目内容
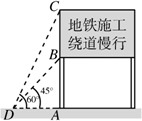 如图,这是交警部门为缓解市区内交通拥挤在学府路某处设立的路况显示牌.立杆AB高度是
如图,这是交警部门为缓解市区内交通拥挤在学府路某处设立的路况显示牌.立杆AB高度是| 3 |
分析:先根据等腰直角三角形两直角边相等可得AD=AB,在Rt△ACD中,利用60°角的正切值求出AC,然后根据BC=AC-AB计算即可.
解答:解:∵AB=
m,∠ADB=45°,
∴AD=AB=
m,
∴tan∠ADC=tan60°=
,
即
=
,
解得AC=3,
∴BC=AC-AB=(3-
)米.
故选B.
| 3 |
∴AD=AB=
| 3 |
∴tan∠ADC=tan60°=
| AC |
| AD |
即
| AC | ||
|
| 3 |
解得AC=3,
∴BC=AC-AB=(3-
| 3 |
故选B.
点评:本题考查了解直角三角形,比较简单,主要利用了等腰直角三角形的性质,60°角的正切值.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
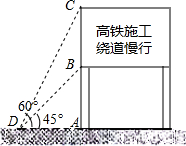 如图,这是交警部门为缓解哈市区内交通拥挤在西大直街某处设立的路况显示牌.立杆AB高度是1米,从D点测得显示牌顶端C和底端B的仰角分别是60°和45°,则BC的长为
如图,这是交警部门为缓解哈市区内交通拥挤在西大直街某处设立的路况显示牌.立杆AB高度是1米,从D点测得显示牌顶端C和底端B的仰角分别是60°和45°,则BC的长为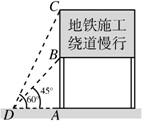 如图,这是交警部门为缓解市区内交通拥挤在学府路某处设立的路况显示牌.立杆AB高度是
如图,这是交警部门为缓解市区内交通拥挤在学府路某处设立的路况显示牌.立杆AB高度是 m,从D点测得显示牌顶端C和底端B的仰角分别是60°和45°,则显示牌BC的高度
m,从D点测得显示牌顶端C和底端B的仰角分别是60°和45°,则显示牌BC的高度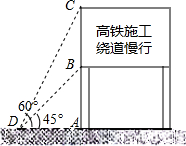 如图,这是交警部门为缓解哈市区内交通拥挤在西大直街某处设立的路况显示牌.立杆AB高度是1米,从D点测得显示牌顶端C和底端B的仰角分别是60°和45°,则BC的长为________米(结果保留根号)
如图,这是交警部门为缓解哈市区内交通拥挤在西大直街某处设立的路况显示牌.立杆AB高度是1米,从D点测得显示牌顶端C和底端B的仰角分别是60°和45°,则BC的长为________米(结果保留根号)