题目内容
某销售公司为了更好地销售某种商品,技术人员对去年三月份至九月份该商品的售价和进价进行了调研.调研结果如下:每件商品的售价M(元)与时间t(月)(3≤t≤9,t为整数)的函数关系式为:M=
;每件商品的成本Q(元)与时间t(月)(3≤t≤9,t为整数)的关系如下表:
根据以上信息解答下列问题:
(1)认真分析上表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的Q与t之间的函数关系式;
(2)按照去年的销售规律,在今年的三月至七月期间,若该公司共有此种商品90000件,准备在一个月内全部销售完,那么在哪个月销售所获利润最小?最小利润是多少?
(3)预计今年十月每件商品的进价将比去年九月减少a%,随即进价将出现反弹,十一月份的进价将在今年十月的基础上增加2a%.而十一月份每件商品的售价将比去年九月增加0.5a%.欲使今年十一月份销售每件产品的利润是去年九月份的1.2倍,试估算a的整数值.(参考数据:482=2304,492=2401,502=2500,512=2601,522=2704)
|
| 时间t(月) | … | 4 | 5 | 6 | 7 | … | ||||||
| 每件进价Q(元) | … |
|
|
4 |
|
… |
(1)认真分析上表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的Q与t之间的函数关系式;
(2)按照去年的销售规律,在今年的三月至七月期间,若该公司共有此种商品90000件,准备在一个月内全部销售完,那么在哪个月销售所获利润最小?最小利润是多少?
(3)预计今年十月每件商品的进价将比去年九月减少a%,随即进价将出现反弹,十一月份的进价将在今年十月的基础上增加2a%.而十一月份每件商品的售价将比去年九月增加0.5a%.欲使今年十一月份销售每件产品的利润是去年九月份的1.2倍,试估算a的整数值.(参考数据:482=2304,492=2401,502=2500,512=2601,522=2704)
分析:(1)设Q与t之间的函数关系式为Q=at2+bt+c,根据统计表中的数据利用待定系数法就可以求出结论;
(2)设在今年的三月至七月期间月销售所获利润为W元,根据题意求出W与t之间的函数关系式,根据函数解析式的性质就可以求出最值;
(3)先根据(1)、(2)的结论求出去年9月的进价为:-
×81+4×9-8=1元,今年11月的进价为1(1-a%)(1+2a%)元,去年九月的售价为:
×9+
=9元,今年11月份的售价为:9(1+0.5a%)元,根据十一月份销售每件产品的利润是去年九月份的1.2倍建立方程求出其解就可以了.
(2)设在今年的三月至七月期间月销售所获利润为W元,根据题意求出W与t之间的函数关系式,根据函数解析式的性质就可以求出最值;
(3)先根据(1)、(2)的结论求出去年9月的进价为:-
| 1 |
| 3 |
| 1 |
| 6 |
| 15 |
| 2 |
解答:解:(1)设Q与t之间的函数关系式为Q=at2+bt+c,由统计表,得
,
解得:
,
∴Q=-
t2+4t-8;
(2)设在今年的三月至七月期间月销售所获利润为W元,由题意,得
W=[(
t+4)-(-
t2+4t-8)]×90000,
=[
t2-
t+12]×90000,
=30000t2-300000+1080000,
=30000(t2-10t)+1080000,
=30000(t-5)2+330000,
∵a=30000>0,
∴抛物线的开口向上,W有最小值,
∴t=5时,W最小值=330000,
∴在5月份销售利润最小,最小利润是330000元;
(3)由题意,得
去年9月的进价为:-
×81+4×9-8=1元,
今年11月的进价为:1(1-a%)(1+2a%)元,
去年九月的售价为:
×9+
=9元,
今年11月份的售价为:9(1+0.5a%)元,
∴9(1+0.5a%)-1(1-a%)(1+2a%)=(9-1)×1.2,
设a%=m,则
9(1+0.5m)-1(1-m)(1+2m)=9.6,
9+4.5m-(1+m-2m2)=9.6,
20m2+35m-16=0,
m=
,
∵502=2500,
∴m=
,
∴m1=0.375,m2=-2.125(舍去),
∴0.375=a%,
∴a=37.5,
∵a为整数,
∴a≈38.
答:a的整数值为38.
|
解得:
|
∴Q=-
| 1 |
| 3 |
(2)设在今年的三月至七月期间月销售所获利润为W元,由题意,得
W=[(
| 2 |
| 3 |
| 1 |
| 3 |
=[
| 1 |
| 3 |
| 10 |
| 3 |
=30000t2-300000+1080000,
=30000(t2-10t)+1080000,
=30000(t-5)2+330000,
∵a=30000>0,
∴抛物线的开口向上,W有最小值,
∴t=5时,W最小值=330000,
∴在5月份销售利润最小,最小利润是330000元;
(3)由题意,得
去年9月的进价为:-
| 1 |
| 3 |
今年11月的进价为:1(1-a%)(1+2a%)元,
去年九月的售价为:
| 1 |
| 6 |
| 15 |
| 2 |
今年11月份的售价为:9(1+0.5a%)元,
∴9(1+0.5a%)-1(1-a%)(1+2a%)=(9-1)×1.2,
设a%=m,则
9(1+0.5m)-1(1-m)(1+2m)=9.6,
9+4.5m-(1+m-2m2)=9.6,
20m2+35m-16=0,
m=
-35±
| ||
| 40 |
∵502=2500,
∴m=
| -35±50 |
| 40 |
∴m1=0.375,m2=-2.125(舍去),
∴0.375=a%,
∴a=37.5,
∵a为整数,
∴a≈38.
答:a的整数值为38.
点评:本题考查了待定系数法求二次函数的解析式的运用,二次函数的顶点式的运用,列一元二次方程解实际问题的运用,解答本题时求出函数的解析式是解第三问的基础,根据十一月份销售每件产品的利润是去年九月份的1.2倍建立方程是求a的值的关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
某销售公司为了更好地销售某种商品,技术人员对去年三月份至九月份该商品的售价和进价进行了调研.调研结果如下:每件商品的售价M(元)与时间t(月)(3≤t≤9,t为整数)的函数关系式为:M=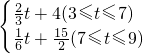 ;每件商品的成本Q(元)与时间t(月)(3≤t≤9,t为整数)的关系如下表:
;每件商品的成本Q(元)与时间t(月)(3≤t≤9,t为整数)的关系如下表:
| 时间t(月) | … | 4 | 5 | 6 | 7 | … |
| 每件进价Q(元) | … |  |  | 4 |  | … |
(1)认真分析上表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的Q与t之间的函数关系式;
(2)按照去年的销售规律,在今年的三月至七月期间,若该公司共有此种商品90000件,准备在一个月内全部销售完,那么在哪个月销售所获利润最小?最小利润是多少?
(3)预计今年十月每件商品的进价将比去年九月减少a%,随即进价将出现反弹,十一月份的进价将在今年十月的基础上增加2a%.而十一月份每件商品的售价将比去年九月增加0.5a%.欲使今年十一月份销售每件产品的利润是去年九月份的1.2倍,试估算a的整数值.(参考数据:482=2304,492=2401,502=2500,512=2601,522=2704)