ЬтФПФкШн
ЁОЬтФПЁПЮЪЬтЗЂЯжЃК
ЃЈ![]() ЃЉШчЭМЂйЃЌЕу
ЃЉШчЭМЂйЃЌЕу![]() ЮЊЦНааЫФБпаЮ
ЮЊЦНааЫФБпаЮ![]() ФквЛЕуЃЌЧыЙ§Еу
ФквЛЕуЃЌЧыЙ§Еу![]() ЛвЛЬѕжБЯп
ЛвЛЬѕжБЯп![]() ЃЌЪЙЦфЭЌЪБЦНЗжЦНааЫФБпаЮ
ЃЌЪЙЦфЭЌЪБЦНЗжЦНааЫФБпаЮ![]() ЕФУцЛ§КЭжмГЄЃЎ
ЕФУцЛ§КЭжмГЄЃЎ
ЮЪЬтЬНОПЃК
ЃЈ![]() ЃЉШчЭМЂкЃЌдкЦНУцжБНЧзјБъЯЕ
ЃЉШчЭМЂкЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌОиаЮ
жаЃЌОиаЮ![]() ЕФБп
ЕФБп![]() ЁЂ
ЁЂ![]() ЗжБ№дк
ЗжБ№дк![]() жсЁЂ
жсЁЂ![]() жсе§АыжсЩЯЃЌЕу
жсе§АыжсЩЯЃЌЕу![]() зјБъЮЊ
зјБъЮЊ![]() ЃЎвбжЊЕу
ЃЎвбжЊЕу![]() ЮЊОиаЮЭтвЛЕуЃЌЧыЙ§Еу
ЮЊОиаЮЭтвЛЕуЃЌЧыЙ§Еу![]() ЛвЛЬѕЭЌЪБЦНЗжОиаЮ
ЛвЛЬѕЭЌЪБЦНЗжОиаЮ![]() УцЛ§КЭжмГЄЕФжБЯп
УцЛ§КЭжмГЄЕФжБЯп![]() ЃЌЫЕУїРэгЩВЂЧѓГіжБЯп
ЃЌЫЕУїРэгЩВЂЧѓГіжБЯп![]() ЃЌЫЕУїРэгЩВЂЧѓГіжБЯп
ЃЌЫЕУїРэгЩВЂЧѓГіжБЯп![]() БЛОиаЮ
БЛОиаЮ![]() НиЕУЯпЖЮЕФГЄЖШЃЎ
НиЕУЯпЖЮЕФГЄЖШЃЎ
ЮЪЬтНтОіЃК
ЃЈ![]() ЃЉШчЭМЂлЃЌдкЦНУцжБНЧзјБъЯЕ
ЃЉШчЭМЂлЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌОиаЮ
жаЃЌОиаЮ![]() ЕФБп
ЕФБп![]() ЁЂ
ЁЂ![]() ЗжБ№дк
ЗжБ№дк![]() жсЁЂ
жсЁЂ![]() жсе§АыжсЩЯЃЌ
жсе§АыжсЩЯЃЌ ![]() жсЃЌ
жсЃЌ ![]() жсЃЌЧв
жсЃЌЧв![]() ЃЌ
ЃЌ ![]() ЃЌЕу
ЃЌЕу![]() ЮЊЮхБпаЮФквЛЕуЃЎЧыЮЪЃКЪЧЗёДцдкЙ§Еу
ЮЊЮхБпаЮФквЛЕуЃЎЧыЮЪЃКЪЧЗёДцдкЙ§Еу![]() ЕФжБЯп
ЕФжБЯп![]() ЃЌЗжБ№гыБп
ЃЌЗжБ№гыБп![]() гы
гы![]() НЛгкЕу
НЛгкЕу![]() ЁЂ
ЁЂ![]() ЃЌЧвЭЌЪБЦНЗжЮхБпаЮ
ЃЌЧвЭЌЪБЦНЗжЮхБпаЮ![]() ЕФУцЛ§КЭжмГЄ?ШєДцдкЃЌЧыЧѓГіЕу
ЕФУцЛ§КЭжмГЄ?ШєДцдкЃЌЧыЧѓГіЕу![]() КЭЕу
КЭЕу![]() ЕФзјБъЃКШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃКШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ



ЁОД№АИЁПЃЈ1ЃЉзїЭММћНтЮіЃЛЃЈ2ЃЉ![]() ЃЌ
ЃЌ ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() ЃЌ
ЃЌ ![]() ЃЎ
ЃЎ
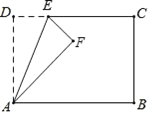
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉСЌНгACЁЂBDНЛгкЕуOЃЌзїжБЯпPOЃЌжБЯпPOНЋЦНааЫФБпаЮABCDЕФУцЛ§КЭжмГЄЗжБ№ЯрЕШЕФСНВПЗжЃЎ
ЃЈ2ЃЉСЌНгACЃЌBDНЛгкЕу![]() ЃЌЙ§
ЃЌЙ§![]() ЁЂPЕуЕФжБЯпНЋОиаЮABCDЕФУцЛ§КЭжмГЄЗжЮЊЗжБ№ЯрЕШЕФСНВПЗжЃЎ
ЁЂPЕуЕФжБЯпНЋОиаЮABCDЕФУцЛ§КЭжмГЄЗжЮЊЗжБ№ЯрЕШЕФСНВПЗжЃЎ
ЃЈ3ЃЉДцдкЃЌжБЯп![]() ЦНЗжЮхБпаЮ
ЦНЗжЮхБпаЮ![]() УцЛ§ЁЂжмГЄЃЎ
УцЛ§ЁЂжмГЄЃЎ
ЪдЬтНтЮіЃКЃЈ![]() ЃЉзїЭМШчЯТЃК
ЃЉзїЭМШчЯТЃК
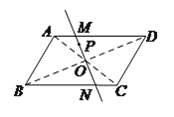
ЃЈ![]() ЃЉЁп
ЃЉЁп![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ
ЁрЩш![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
НЛ![]() жсгк
жсгк![]() ЃЌ
ЃЌ
НЛ![]() гк
гк![]() ЃЌ
ЃЌ
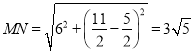 ЃЎ
ЃЎ

ЃЈ![]() ЃЉДцдкЃЌжБЯп
ЃЉДцдкЃЌжБЯп![]() ЦНЗжЮхБпаЮ
ЦНЗжЮхБпаЮ![]() УцЛ§ЁЂжмГЄЃЎ
УцЛ§ЁЂжмГЄЃЎ
Ёп![]() дкжБЯп
дкжБЯп![]() ЩЯЃЌ
ЩЯЃЌ
ЁрСЌ![]() НЛ
НЛ![]() ЁЂ
ЁЂ![]() гкЕу
гкЕу![]() ЁЂ
ЁЂ![]() ЃЌ
ЃЌ
Щш![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ
ЁржБЯп![]() ЃЌ
ЃЌ
СЊСЂ![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ ![]() ЃЎ
ЃЎ

 зДдЊМАЕкЯЕСаД№АИ
зДдЊМАЕкЯЕСаД№АИ ЭЌВНАТЪ§ЯЕСаД№АИ
ЭЌВНАТЪ§ЯЕСаД№АИЁОЬтФПЁПФГаЃЩфЛїЖгДгМзЁЂввЁЂБћЁЂЖЁЫФШЫжабЁАЮвЛШЫВЮМгЪадЫЛсЩфЛїБШШќЃЎдкбЁАЮШќжаЃЌУПШЫЩфЛї10ДЮЃЌЫћУЧ10ДЮГЩМЈЕФЦНОљЪ§МАЗНВюШчЯТБэЫљЪОЃЎ
Мз | вв | Бћ | ЖЁ | |
ЦНОљЪ§/ЛЗ | 9.7 | 9.5 | 9.5 | 9.7 |
ЗНВю/ЛЗ2 | 5.1 | 4.7 | 4.5 | 4.5 |
ЧыФуИљОнБэжаЪ§ОнбЁвЛШЫВЮМгБШШќЃЌзюКЯЪЪЕФШЫбЁЪЧ ЃЎ