题目内容
通过计算,比较下列各组中两个数的大小(在空格内填“<”“>”“=”)(1)12
(2)、从第1题的结果经过归纳,可猜想出nn+1和( n+1)n的大小关系是.
(3)、根据上面的归纳猜想得到的一般结论,试比较下面两数的大小.
20022003
27、如图,将一张正方形纸片,剪成四个大小形状一样的小正方形,然后将其中的一个小正方形再按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去;
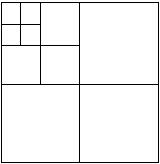
(1)填表:

(2)请你推断,能不能按上述操作过程,将原来的正方形剪成99个小正方形?为什么?
(3)观察图形,你还能得出什么规律?
分析:(1)①通过计算,可以比较大小;
②由①的特例可以看出:当n<3时,nn+1<( n+1)n;当n≥3时,nn+1>( n+1)n;
③由②的规律直接得出结论;
(2)①第一次是4个,以后每一次都少1多4(即多3个),照此填表即可;
②由表中的数据规律列方程解答即可;
③可以求剪后的每个小正方形的面积是与原来正方形面积的几分之几.
②由①的特例可以看出:当n<3时,nn+1<( n+1)n;当n≥3时,nn+1>( n+1)n;
③由②的规律直接得出结论;
(2)①第一次是4个,以后每一次都少1多4(即多3个),照此填表即可;
②由表中的数据规律列方程解答即可;
③可以求剪后的每个小正方形的面积是与原来正方形面积的几分之几.
解答:解:(一)(1)依次填<,<,>,>,>,…;
(2)由(1)可知当n<3时,nn+1<( n+1)n;当n≥3时,nn+1>( n+1)n;
(3)因为2002+1=2003,2002>3,
所以20022003>20032002;
故填>.
(二)(1)填表如下:
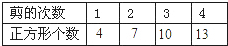
(2)不能按上述操作过程,将原来的正方形剪成99个小正方形;
因为:由(1)可知:3n+1=99,
解得n=
,不合题意.
(3)由图可知剪n次后一个小正方形的面积是原正方形面积的
.
(2)由(1)可知当n<3时,nn+1<( n+1)n;当n≥3时,nn+1>( n+1)n;
(3)因为2002+1=2003,2002>3,
所以20022003>20032002;
故填>.
(二)(1)填表如下:

(2)不能按上述操作过程,将原来的正方形剪成99个小正方形;
因为:由(1)可知:3n+1=99,
解得n=
| 98 |
| 3 |
(3)由图可知剪n次后一个小正方形的面积是原正方形面积的
| 1 |
| 2n+2 |
点评:第一题是由特殊值推出一般规律,第二题是由图形的变化推出一般规律,进一步利用所得规律解答问题.

练习册系列答案
相关题目