题目内容
(2013•汕头)有一副直角三角板,在三角板ABC中,∠BAC=90°,AB=AC=6,在三角板DEF中,∠FDE=90°,DF=4,DE=4
.将这副直角三角板按如图1所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.
(1)如图2,当三角板DEF运动到点D到点A重合时,设EF与BC交于点M,则∠EMC=
(2)如图3,当三角板DEF运动过程中,当EF经过点C时,求FC的长;
(3)在三角板DEF运动过程中,设BF=x,两块三角板重叠部分的面积为y,求y与x的函数解析式,并求出对应的x取值范围.

| 3 |
(1)如图2,当三角板DEF运动到点D到点A重合时,设EF与BC交于点M,则∠EMC=
15
15
度;(2)如图3,当三角板DEF运动过程中,当EF经过点C时,求FC的长;
(3)在三角板DEF运动过程中,设BF=x,两块三角板重叠部分的面积为y,求y与x的函数解析式,并求出对应的x取值范围.

分析:(1)如题图2所示,由三角形的外角性质可得;
(2)如题图3所示,在Rt△ACF中,解直角三角形即可;
(3)认真分析三角板的运动过程,明确不同时段重叠图形的变化情况:
(I)当0≤x≤2时,如答图1所示;
(II)当2<x≤6-2
时,如答图2所示;
(III)当6-2
<x≤6时,如答图3所示.
(2)如题图3所示,在Rt△ACF中,解直角三角形即可;
(3)认真分析三角板的运动过程,明确不同时段重叠图形的变化情况:
(I)当0≤x≤2时,如答图1所示;
(II)当2<x≤6-2
| 3 |
(III)当6-2
| 3 |
解答:解:(1)如题图2所示,
∵在三角板DEF中,∠FDE=90°,DF=4,DE=4
,
∴tan∠DFE=
=
,∴∠DFE=60°,
∴∠EMC=∠FMB=∠DFE-∠ABC=60°-45°=15°;
(2)如题图3所示,当EF经过点C时,
FC=
=
=
=4
;
(3)在三角板DEF运动过程中,
(I)当0≤x≤2时,如答图1所示:
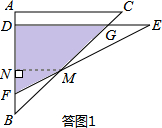
设DE交BC于点G.
过点M作MN⊥AB于点N,则△MNB为等腰直角三角形,MN=BN.
又∵NF=
=
MN,BN=NF+BF,
∴NF+BF=MN,即
MN+x=MN,解得:MN=
x.
y=S△BDG-S△BFM
=
BD•DG-
BF•MN
=
(x+4)2-
x•
x
=-
x2+4x+8;
(II)当2<x≤6-2
时,如答图2所示:

过点M作MN⊥AB于点N,则△MNB为等腰直角三角形,MN=BN.
又∵NF=
=
MN,BN=NF+BF,
∴NF+BF=MN,即
MN+x=MN,解得:MN=
x.
y=S△ABC-S△BFM
=
AB•AC-
BF•MN
=
×62-
x•
x
=-
x2+18;
(III)当6-2
<x≤6时,如答图3所示:

由BF=x,则AF=AB-BF=6-x,
设AC与EF交于点M,则AM=AF•tan60°=
(6-x).
y=S△AFM=
AF•AM=
(6-x)•
(6-x)=
x2-6
x+18
.
综上所述,y与x的函数解析式为:
y=
.
∵在三角板DEF中,∠FDE=90°,DF=4,DE=4
| 3 |
∴tan∠DFE=
| DE |
| DF |
| 3 |
∴∠EMC=∠FMB=∠DFE-∠ABC=60°-45°=15°;
(2)如题图3所示,当EF经过点C时,
FC=
| AC |
| sin∠AFC |
| 6 |
| sin60° |
| 6 | ||||
|
| 3 |
(3)在三角板DEF运动过程中,
(I)当0≤x≤2时,如答图1所示:

设DE交BC于点G.
过点M作MN⊥AB于点N,则△MNB为等腰直角三角形,MN=BN.
又∵NF=
| MN |
| tan60° |
| ||
| 3 |
∴NF+BF=MN,即
| ||
| 3 |
3+
| ||
| 2 |
y=S△BDG-S△BFM
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
3+
| ||
| 2 |
=-
| ||
| 4 |
(II)当2<x≤6-2
| 3 |

过点M作MN⊥AB于点N,则△MNB为等腰直角三角形,MN=BN.
又∵NF=
| MN |
| tan60° |
| ||
| 3 |
∴NF+BF=MN,即
| ||
| 3 |
3+
| ||
| 2 |
y=S△ABC-S△BFM
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
3+
| ||
| 2 |
=-
3+
| ||
| 4 |
(III)当6-2
| 3 |

由BF=x,则AF=AB-BF=6-x,
设AC与EF交于点M,则AM=AF•tan60°=
| 3 |
y=S△AFM=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 3 |
| 3 |
综上所述,y与x的函数解析式为:
y=
|
点评:本题是运动型综合题,解题关键是认真分析三角板的运动过程,明确不同时段重叠图形形状的变化情况.在解题计算过程中,除利用三角函数进行计算外,也可以利用三角形相似,殊途同归.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目