题目内容
如图(1),矩形纸片ABCD中,AD=28cm,AB=20cm.(1)将矩形ABCD沿折线AE对折,使AB与AD边重合,B点落在F点处(如图(2)所示);再剪去四边形CEFD,余下的部分如图(3)所示.若将余下的纸片展形,则所得的四边形ABEF的形状是
(2)将图(3)中的纸片沿折线AG对折,使AF与AE边重合,F点落在H点处(如图(4)所示),再沿HG将△HE剪去,余下的部分如图(5)所示.把图(5)的纸片完全展开,请你在图(6)的矩形ABCD中画出展开后图形的示意图,剪去的部分用阴影表示,折痕用虚线表示.
(3)求图(5)中的纸片完全展形后图形的面积(结果保留整数).
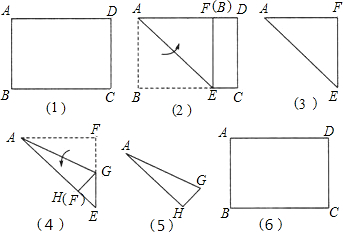
分析:(1)由图形翻折变换的性质可知AF=AB,再根据AB=20cm即可得出结论;
(2)根据题意画出图形即可;
(3)先根据勾股定理求出AE的长,由图形折叠的性质可知GF=GH,AF=AH,设GF=x,利用勾股定理可求出x的值,进而可得出△GHE的面积,进而可得出结论.
(2)根据题意画出图形即可;
(3)先根据勾股定理求出AE的长,由图形折叠的性质可知GF=GH,AF=AH,设GF=x,利用勾股定理可求出x的值,进而可得出△GHE的面积,进而可得出结论.
解答:解:(1)∵△AEF是△AEB翻折而成,
∴AB=AF,
∵AB=20cm,
∴AF=20cm,
∵四边形ABCD是矩形,
∴∠ABE=∠AFE,
∴四边形ABEF是正方形,面积为:400cm2;
(2)
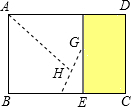
(3)由图形翻折变换的性质可知,GF=GH,AF=AH,
∵AF=EF=20cm,
∴AE=
=20
cm,
设GF=x,则HG=x,GE=20-x,HE=AE-AH=20
-20,
在Rt△EGH中,GE2=HG2+HE2,即(20-x)2=x2+(20
-20)2,解得x=20
-20,
∴S△GHE=
HE•HG=
×(20
-20)×(20
-20)=600-400
,
∴减去的直角三角形展开后的面积=2S△GHE=2×(600-400
)=1200-800
,
∴剩余图形展开后的面积=S□ABEF-22S△GHE=400-1200+800
=800
-800≈800×1.4-800=320.
∴AB=AF,
∵AB=20cm,
∴AF=20cm,
∵四边形ABCD是矩形,
∴∠ABE=∠AFE,
∴四边形ABEF是正方形,面积为:400cm2;
(2)

(3)由图形翻折变换的性质可知,GF=GH,AF=AH,
∵AF=EF=20cm,
∴AE=
| 202+202 |
| 2 |
设GF=x,则HG=x,GE=20-x,HE=AE-AH=20
| 2 |
在Rt△EGH中,GE2=HG2+HE2,即(20-x)2=x2+(20
| 2 |
| 2 |
∴S△GHE=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
∴减去的直角三角形展开后的面积=2S△GHE=2×(600-400
| 2 |
| 2 |
∴剩余图形展开后的面积=S□ABEF-22S△GHE=400-1200+800
| 2 |
| 2 |
点评:本题考查的是图形的翻折变换,熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解答此题的关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目

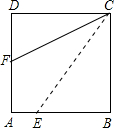 如图,将一张矩形纸片ABCD沿CE折叠,B点恰好落在AD边上,设此点为F,若AB:BC=4:5,则sin∠CFD=
如图,将一张矩形纸片ABCD沿CE折叠,B点恰好落在AD边上,设此点为F,若AB:BC=4:5,则sin∠CFD= 如图所示,把矩形纸片ABCD,沿EF对折,若∠BFG=40°,则∠DEF=
如图所示,把矩形纸片ABCD,沿EF对折,若∠BFG=40°,则∠DEF=