题目内容
小强在劳动技术课中要制作一个周长为80cm的等腰三角形.请你写出底边长y（cm）与一腰长x（cm）的函数关系式，并求出自变量的取值范围.
【答案】
，
.
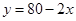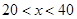【解析】
试题分析：我们知道等腰三角形的周长=腰长×2+底长．据此可得出函数关系式．求自变量的取值范围时可根据三角形的三边关系来解（三角形两边的和大于第三边，两边的差小于第三边）．
由三角形的周长公式可得：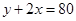
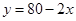，即；但由于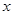
、
的取值范围受到图形的限制：一方面，由
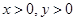，即
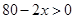，可确定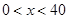
；另一方面，由三角形三边关系定理及其推论（三角形两边之和大于第三边、三角形两边之差小于第三边）得
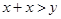，即
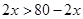，解得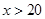
.故的取值范围是.
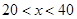考点：本题考查的是列函数关系式
点评：本题中求自变量的取值范围时要注意三角形三边关系的运用．
练习册系列答案
相关题目