题目内容
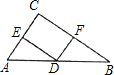 D、E、F分别为△ABC的边AB、AC,BC的中点,且DF=3,DE=4,AB=10.判断△ABC的形状________.
D、E、F分别为△ABC的边AB、AC,BC的中点,且DF=3,DE=4,AB=10.判断△ABC的形状________.
直角三角形
分析:先根据三角形中位线定理先求出AC、BC的长,再根据勾股定理的逆定理判断△ABC的形状.
解答:∵D、E、F分别为△ABC的边AB、AC,BC的中点,且DF=3,DE=4,AB=10,
∴AC=6、BC=8,
又∵62+82=102,
故△ABC的形状是直角三角形.
故答案为直角三角形.
点评:本题考查了三角形中位线定理及勾股定理的逆定理.
三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.
分析:先根据三角形中位线定理先求出AC、BC的长,再根据勾股定理的逆定理判断△ABC的形状.
解答:∵D、E、F分别为△ABC的边AB、AC,BC的中点,且DF=3,DE=4,AB=10,
∴AC=6、BC=8,
又∵62+82=102,
故△ABC的形状是直角三角形.
故答案为直角三角形.
点评:本题考查了三角形中位线定理及勾股定理的逆定理.
三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
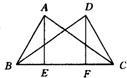 12、如图所示,△ABC和△DCB有公共边BC,且AB=DC,作AE⊥BC,DF⊥BC,垂足分别为E、F,AE=DF,那么求证AC=BD时,需要证明三角形全等的三角形是
12、如图所示,△ABC和△DCB有公共边BC,且AB=DC,作AE⊥BC,DF⊥BC,垂足分别为E、F,AE=DF,那么求证AC=BD时,需要证明三角形全等的三角形是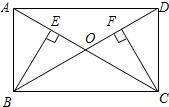 21、如图,矩形ABCD中,AC与BD交于点O,BE⊥AC,CF⊥BD,垂足分别为E,F.
21、如图,矩形ABCD中,AC与BD交于点O,BE⊥AC,CF⊥BD,垂足分别为E,F.