题目内容
若一元二次方程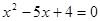 的两根是等腰△ABC的两边,则△ABC的周长为_________。
的两根是等腰△ABC的两边,则△ABC的周长为_________。
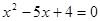 的两根是等腰△ABC的两边,则△ABC的周长为_________。
的两根是等腰△ABC的两边,则△ABC的周长为_________。9
由因式分解的方法即可求得x2-5x+4=0的两根,然后又由三边关系,即可求得答案.
解:∵x2-5x+4=0,
∴(x-1)(x-4)=0,
解得:x1=1,x2=4,
∵一元二次方程x2-5x+4=0的两根是等腰△ABC的两边,
当1是腰长,底边等于4时,
∵1+1<4,
∴不能组成三角形(舍去);
当4是腰长,底边等于1时,
∵4,4,1能组成三角形,
∴△ABC的周长为:9.
故答案为:9.
题考查了因式分解法解一元二次方程、三角形三边关系以及等腰三角形的性质.此题难度不大,注意三边关系的应用.
解:∵x2-5x+4=0,
∴(x-1)(x-4)=0,
解得:x1=1,x2=4,
∵一元二次方程x2-5x+4=0的两根是等腰△ABC的两边,
当1是腰长,底边等于4时,
∵1+1<4,
∴不能组成三角形(舍去);
当4是腰长,底边等于1时,
∵4,4,1能组成三角形,
∴△ABC的周长为:9.
故答案为:9.
题考查了因式分解法解一元二次方程、三角形三边关系以及等腰三角形的性质.此题难度不大,注意三边关系的应用.

练习册系列答案
相关题目
 ,
, 是方程
是方程 的两个根,则
的两个根,则 =
= 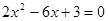 ,圆心距为
,圆心距为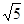 ,则两圆的位置关系为 ( )
,则两圆的位置关系为 ( )
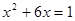 小题4:用配方法解方程:x2-4x+1=0
小题4:用配方法解方程:x2-4x+1=0
