题目内容
【题目】如图,抛物线y=ax2+2x+c经过点A(0,3)、B(﹣1,0),请解答下列问题:
(1)求抛物线的解析式;
(2)抛物线的顶点为D,与x轴的另一交点为C,对称轴交x轴于点E,连接BD,求cos∠DBE;
(3)在直线BD上是否存在点F,使由B、C、F三点构成的三角形与△BDE相似?若存在,求出点F的坐标;若不存在,请说明理由.
【答案】
(1)
解:将A(0,3)、B(﹣1,0)代入y=ax2+2x+c可得:
c=3,a=﹣1,
抛物线的解析式为y=﹣x2+2x+3
(2)
解:∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴D(1,4),
∴BE=2,DE=4,
∴BD= ![]() =2
=2 ![]() ,
,
∴cos∠DBE= ![]() =
= ![]()
(3)
解:∵B(﹣1,0),D(1,4),
∴直线BD的解析式为y=2x+2,
∵y=﹣x2+2x+3=﹣(x﹣3)(x+1),
∴C(3,0),
∴BC=4,
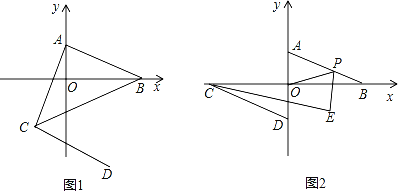
①若△BED∽△BFC,如图1,

则∠BED=∠BFC=90°,
作FG⊥BC于G,
∵cos∠CBF= ![]() ,
,
∴BF= ![]() ,
,
∴BG= ![]() =
= ![]() ,
,
∴OG= ![]() ,GF=
,GF= ![]() ,
,
∴F(﹣ ![]() ,
, ![]() );
);
②若△BED∽△BCF,如图2,

则∠BCF=90°,
∴F点横坐标为3,
将3代入BD解析式得:y=8,
∴F(3,8);
综上所述,满足要求的F点的坐标为:(﹣ ![]() ,
, ![]() )、(3,8)
)、(3,8)
【解析】(1)将A、B两点坐标代入即可求得解析式;(2)先求出D点坐标,从而求出BE、DE、BD长度,cos∠DBE则可直接算出;(3)由于B是公共点,不可能是直角顶点,所以就只剩下两种情,即让C和F分别为直角顶点,根据相似性质,列出比例等式计算即可.
【考点精析】利用二次函数的图象和二次函数的性质对题目进行判断即可得到答案,需要熟知二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案【题目】某班10名学生的校服尺寸与对应人数如表所示:
尺寸(cm) | 160 | 165 | 170 | 175 | 180 |
学生人数(人) | 1 | 3 | 2 | 2 | 2 |
则这10名学生校服尺寸的众数和中位数分别为( )
A.165cm,165cm
B.165cm,170cm
C.170cm,165cm
D.170cm,170cm
【题目】下表中有两种移动电话计费方式.
月使用费 | 主叫限定时间 | 主叫超时费 | 被叫 | |
方式一 | 49 | 100 |
| 免费 |
方式二 | 69 | 150 |
| 免费 |
设一个月内主叫通话为t分钟![]() 是正整数
是正整数![]() .
.
![]() 当
当![]() 时,按方式一计费为______元;按方式二计费为______元;
时,按方式一计费为______元;按方式二计费为______元;
![]() 当
当![]() 时,是否存在某一时间t,使两种计费方式相等,若存在,请求出对应t的值,若不存在,请说明理由;
时,是否存在某一时间t,使两种计费方式相等,若存在,请求出对应t的值,若不存在,请说明理由;
![]() 当
当![]() 时,请直接写出省钱的计费方式?
时,请直接写出省钱的计费方式?