题目内容
学习与探究:
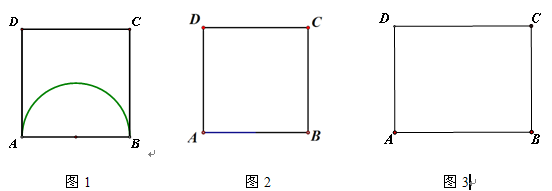
(1)请在图1的正方形ABCD中,作出使∠APB=90°的所有点P,并简要说明做法.我们可以这样解决问题:利用直径所对的圆周角等于90°,作以AB为直径的圆,则正方形ABCD内部的半圆上所有点(A、B除外)为所求.
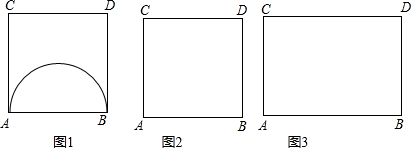
(2)请在图2的正方形ABCD内(含边),画出使∠APB=60°的所有的点P,尺规作图,不写作法,保留痕迹;
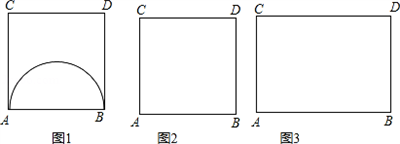
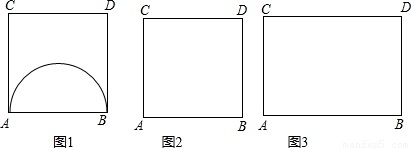
(3)如图3,已知矩形ABCD中,AB=4,AC=3,请在矩形内(含边),画出∠APB=60°的所有的点P,尺规作图,不写作法,保留痕迹.
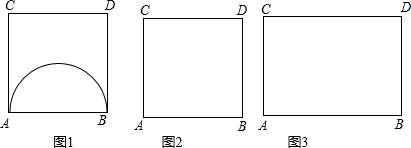
(1)请在图1的正方形ABCD中,作出使∠APB=90°的所有点P,并简要说明做法.我们可以这样解决问题:利用直径所对的圆周角等于90°,作以AB为直径的圆,则正方形ABCD内部的半圆上所有点(A、B除外)为所求.
(2)请在图2的正方形ABCD内(含边),画出使∠APB=60°的所有的点P,尺规作图,不写作法,保留痕迹;
(3)如图3,已知矩形ABCD中,AB=4,AC=3,请在矩形内(含边),画出∠APB=60°的所有的点P,尺规作图,不写作法,保留痕迹.

分析:(1)利用直径所对圆周角等于90°,即可得出;
(2)①以AB为边在正方形内作等边△ABP;
②作△ABP的外接圆⊙O,分别与AD、BC交于点E、F,由于在⊙O中,弦AB所对的
上的圆周角均为60°,所以
上的所有点均为所求的点P.
(3)因为∠APB=∠CP'D=60°,△APB和△CP′D的面积最大,所以同(2):
①连接AC;②以AB为边作等边△ABE;③作等边△ABE的外接圆O,交AC于点P;④在AC上截取AP'=CP.则点P、P′为所求.
(2)①以AB为边在正方形内作等边△ABP;
②作△ABP的外接圆⊙O,分别与AD、BC交于点E、F,由于在⊙O中,弦AB所对的
 |
| APB |
 |
| EF |
(3)因为∠APB=∠CP'D=60°,△APB和△CP′D的面积最大,所以同(2):
①连接AC;②以AB为边作等边△ABE;③作等边△ABE的外接圆O,交AC于点P;④在AC上截取AP'=CP.则点P、P′为所求.
解答: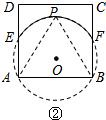 解:(1)在以AB为直径的半圆上,A,B两点除外;
解:(1)在以AB为直径的半圆上,A,B两点除外;
(2)如图②,
作△ABP的外接圆⊙O,分别与AD、BC交于点E、F,弧EF上所有的点均可.
理由:同圆中同弧所对的圆周角相等,
(3)如图③,画法如图: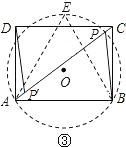
①连接AC;
②以AB为边作等边△ABE;
③作等边△ABE的外接圆O,交AC于点P;
④在AC上截取AP'=CP.则点P、P′为所求.
(评卷时,作图准确,无画法的不扣分)
 解:(1)在以AB为直径的半圆上,A,B两点除外;
解:(1)在以AB为直径的半圆上,A,B两点除外;(2)如图②,
作△ABP的外接圆⊙O,分别与AD、BC交于点E、F,弧EF上所有的点均可.
理由:同圆中同弧所对的圆周角相等,
(3)如图③,画法如图:

①连接AC;
②以AB为边作等边△ABE;
③作等边△ABE的外接圆O,交AC于点P;
④在AC上截取AP'=CP.则点P、P′为所求.
(评卷时,作图准确,无画法的不扣分)
点评:此题主要考查了应用设计与作图,综合利用正方形的性质和同圆中同弧所对的圆周角相等得知识点是解题关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 内,作出使
内,作出使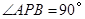 的所有点
的所有点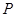 ,并简要说明作法.
,并简要说明作法.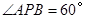 的所有的点
的所有的点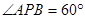 的所有的点
的所有的点