Question

27、已知等边△ABC，求平面内一点P，满足A，B，C，P四点中的任意三点连线都构成等腰三角形．这样的点有

10

个．

Answer 1

分析：（1）点P在三角形的内部时，点P到△ABC的三个顶点的距离相等，所以点P是三角形的外心；
（2）点P在三角形的外部时，每条边的垂直平分线上的点只要能够使顶点这条边的两端点连接而成的三角形是等腰三角形即可．

解答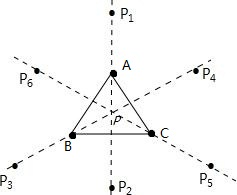：解：（1）点P在三角形内部时，点P是边AB、BC、CA的垂直平分线的交点，是三角形的外心，
（2）点P在三角形外部时，一个对称轴上有三个点，如图：
共有9个点符合要求，
∴具有这种性质的点P共有10个．
故答案为10．

点评：本题主要考查了等腰三角形的的性质，要注意分点在三角形内部和三角形外部两种情况讨论，思考全面是正确解答本题的关键，难度适中．