题目内容
某服装经销商,库存有A品牌服装1200套,每套进价400元,正常销售时每套600元,每月卖100套,一年内刚好卖完.现在市场上流行B品牌服装,此品牌服装进价每套200元,售价每套500元,每月可卖120套,经销商想代理B品牌服装,但无资金流动,只有低价转让A品牌服装,转让价格与转让数量有如下关系:
| 转让数量(套) | 1200 | 1100 | 1000 | 900 | 800 | 700 | 600 | 500 | 400 | 300 | 200 | 100 |
| 转让价格(元/套) | 240 | 250 | 260 | 270 | 280 | 290 | 300 | 310 | 320 | 330 | 340 | 350 |
方案1:全部转让A品牌服装,用转让所得资金购进B品牌服装后,经销B品牌服装.
方案2:部分转让A品牌服装,用转让所得资金购进B品牌服装后,经销B品牌服装,同时也经销A品牌服装.
求:
(1)经销商选择方案1,一年内可获得利润多少元?
(2)经销商选择方案2,转让A品牌服装的数量是多少时,可以使自己在一年内获得最多利润?最多利润是多少元?
解:(1)若选方案一,得转让款1200×240=288000(元),
可购进B品牌服装288000÷200=1440(套)
一年内刚好卖完,
可获利1440×500-480000=240000(元);
(2)设转让A品牌服装x套,则转让价是每套(360- )元
)元
可得转让资金x(360- )元
)元
那么可购进B品牌服装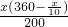 套,
套,
全部售出B品牌服装后得款500×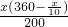 =
= x(360-
x(360- ),
),
此时,还剩A品牌服装(1200-x)套,
全部售出A品牌服装后得款600(1200-x)(元)
共获利: x(360-
x(360- )+600(1200-x)-480000=-
)+600(1200-x)-480000=- ( x-600)2+330000,
( x-600)2+330000,
故当x=600(套),可获最大利润330000元.
答:选择第二种方案在一年内获得利润最大,当他转让给经销商乙的A品牌服装的数量是600套时,可获最大利润330000元.
分析:(1)由全部转让A品牌服装,用转让得来的资金一次性购入B品牌服装后,经销B品牌服装,首先求得转让款,又分析可得可购进B品牌服装,一年内刚好卖完,根据利润的求解方法求得答案;
(2)设转让A品牌服装x套,则转让价格是每套(360- )元,可进购B品牌服装
)元,可进购B品牌服装 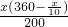 套,列出利润与x之间的函数关系式,求其最大值,即可求得答案.
套,列出利润与x之间的函数关系式,求其最大值,即可求得答案.
点评:本题主要考查了二次函数的实际应用问题.此题难度较大,解题的关键是理解题意,根据利润=(售价-成本)×销售量,列出函数关系式,求出最值,注意灵活运用二次函数解决实际问题.
可购进B品牌服装288000÷200=1440(套)
一年内刚好卖完,
可获利1440×500-480000=240000(元);
(2)设转让A品牌服装x套,则转让价是每套(360-
 )元
)元可得转让资金x(360-
 )元
)元 那么可购进B品牌服装
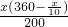 套,
套,全部售出B品牌服装后得款500×
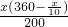 =
= x(360-
x(360- ),
),此时,还剩A品牌服装(1200-x)套,
全部售出A品牌服装后得款600(1200-x)(元)
共获利:
 x(360-
x(360- )+600(1200-x)-480000=-
)+600(1200-x)-480000=- ( x-600)2+330000,
( x-600)2+330000,故当x=600(套),可获最大利润330000元.
答:选择第二种方案在一年内获得利润最大,当他转让给经销商乙的A品牌服装的数量是600套时,可获最大利润330000元.
分析:(1)由全部转让A品牌服装,用转让得来的资金一次性购入B品牌服装后,经销B品牌服装,首先求得转让款,又分析可得可购进B品牌服装,一年内刚好卖完,根据利润的求解方法求得答案;
(2)设转让A品牌服装x套,则转让价格是每套(360-
 )元,可进购B品牌服装
)元,可进购B品牌服装 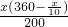 套,列出利润与x之间的函数关系式,求其最大值,即可求得答案.
套,列出利润与x之间的函数关系式,求其最大值,即可求得答案.点评:本题主要考查了二次函数的实际应用问题.此题难度较大,解题的关键是理解题意,根据利润=(售价-成本)×销售量,列出函数关系式,求出最值,注意灵活运用二次函数解决实际问题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
某服装经销商,库存有A品牌服装1200套,每套进价400元,正常销售时每套600元,每月卖100套,一年内刚好卖完.现在市场上流行B品牌服装,此品牌服装进价每套200元,售价每套500元,每月可卖120套,经销商想代理B品牌服装,但无资金流动,只有低价转让A品牌服装,转让价格与转让数量有如下关系:
经销商面临两种选择:
方案1:全部转让A品牌服装,用转让所得资金购进B品牌服装后,经销B品牌服装.
方案2:部分转让A品牌服装,用转让所得资金购进B品牌服装后,经销B品牌服装,同时也经销A品牌服装.
求:
(1)经销商选择方案1,一年内可获得利润多少元?
(2)经销商选择方案2,转让A品牌服装的数量是多少时,可以使自己在一年内获得最多利润?最多利润是多少元?
| 转让数量(套) | 1200 | 1100 | 1000 | 900 | 800 | 700 | 600 | 500 | 400 | 300 | 200 | 100 |
| 转让价格(元/套) | 240 | 250 | 260 | 270 | 280 | 290 | 300 | 310 | 320 | 330 | 340 | 350 |
方案1:全部转让A品牌服装,用转让所得资金购进B品牌服装后,经销B品牌服装.
方案2:部分转让A品牌服装,用转让所得资金购进B品牌服装后,经销B品牌服装,同时也经销A品牌服装.
求:
(1)经销商选择方案1,一年内可获得利润多少元?
(2)经销商选择方案2,转让A品牌服装的数量是多少时,可以使自己在一年内获得最多利润?最多利润是多少元?