题目内容
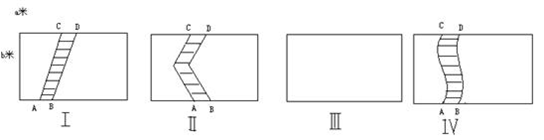
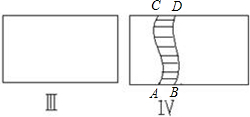
24、如图，在一块长为am、宽为bm的长方形草地上，有如图所示的一处处宽皆1m的小路（即图中阴影部分）
（1）图Ⅰ中，草地面积为
（2）小路的形状如图Ⅳ所示，且每一处的水平宽度皆为1m，则图中草地的面积为
（1）图Ⅰ中，草地面积为
ab-b
，在Ⅱ图中，草地面积为ab-b
，在图Ⅲ中画出有两个折点的小路，并用阴影把它表示出来，则在图Ⅲ中草地面积为ab-b
．（2）小路的形状如图Ⅳ所示，且每一处的水平宽度皆为1m，则图中草地的面积为
ab-b
，请说明理由．分析：（1）在前面2个图形中，常规的办法是利用平行四边形的面积计算来求阴影部分的面积，进而计算空白部分的面积．
（2）当阴影部分的左右边界由折线变为任意曲线时，计算的方法已经不在适用．因此外面考虑图形的拆分和拼凑．利用平移得到空白部分构成的简单图形来计算草地的面积．
（2）当阴影部分的左右边界由折线变为任意曲线时，计算的方法已经不在适用．因此外面考虑图形的拆分和拼凑．利用平移得到空白部分构成的简单图形来计算草地的面积．
解答：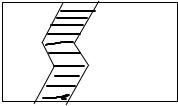
解：（1）ab-b，ab-b，ab-b
（2）ab-b，长方形面积为ab，小路宽AB=1，AB与CD之间距离为b，
∴草地面积为ab-1×b=ab-b．
解：（1）ab-b，ab-b，ab-b（2）ab-b，长方形面积为ab，小路宽AB=1，AB与CD之间距离为b，
∴草地面积为ab-1×b=ab-b．
点评：本题主要考查了矩形的性质和平移的性质．能利用平移的性质把不规则的图形拆分或拼凑为简单图形来计算草地的面积是解题的关键．
练习册系列答案
相关题目
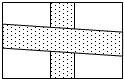
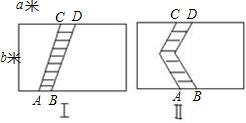
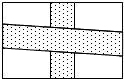为了交通方便，在一块长为am，宽为bm的长方形稻田内修两条道路，横向道路为矩形，纵向道路为平行四边形，道路的宽均为1m（如图），则余下可耕种土地的面积是________m2．
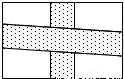为了交通方便，在一块长为am，宽为bm的长方形稻田内修两条道路，横向道路为矩形，纵向道路为平行四边形，道路的宽均为1m（如图），则余下可耕种土地的面积是 m2．