题目内容
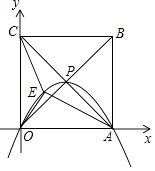
【题目】如图,形如量角器的半圆O的直径DE=12cm,形如三角板的△ABC中,∠ACB=90°,∠ABC=30°, BC=12cm,半圆O以 2cm/s 的速度从左向右运动,在运动过程中,点 D 、E 始终在直线BC 上.设运动时间为t(s) ,当t=0s时,半圆O在△ABC的左侧,OC=8cm。
(1)当t =(s)时,⊙O与AC所在直线第一次相切,点 C 到直线 AB 的距离为;
(2)当 t为何值时,直线 AB 与半圆O所在的圆相切;
(3)当△ABC的一边所在直线与圆O相切时,若⊙O与△ABC有重叠部分,求重叠部分的面积.
【答案】
(1)1.,6.
(2)解:如图2: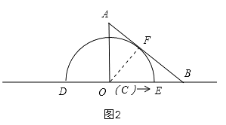
过点C作CF⊥AB于点F,
∴OF=6,
当直线AB于半圆O所在的圆相切时,
∵圆心O到AB的距离为6,半圆的半径为6,且圆心O又在BC上,
∴点O与点C重合,
即当点O运动到点C时,半圆O与![]() ABC的边AB相切,此时点O运动了8cm,t=8
ABC的边AB相切,此时点O运动了8cm,t=8![]() 2=4,
2=4,
如图3: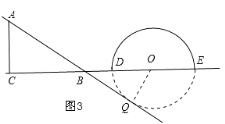
当点O运动到点B的右侧时,且OB=12 ,
过点O作OQ⊥AB于点Q,
在Rt![]() OQB中,∠OBQ=30°,则OQ=
OQB中,∠OBQ=30°,则OQ=![]() OB=6,
OB=6,
即OQ与半圆O所在的圆相切,此时点O运动了12+12+8=32cm,t=32![]() 2=16,
2=16,
综上,当t为4秒或6秒时,直线 AB 与半圆O所在的圆相切.
(3)解:①当半圆O与AB边相切于点F时,如图2: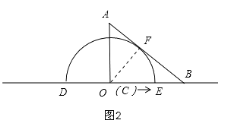
重叠部分的面积S=![]() 62=9
62=9![]() ;
;
②当半圆O与AC相切与点C时,如图4: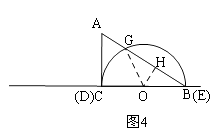
连接OG,
∵BC=DE=12,
∴点C与点D重合,点E与点B重合,
∵OG=OB,
∴∠ABC=∠OGB=30°,
∴∠COG=60°,
过点O作OH⊥AB于点H,
∵OB=6,
∴OH=![]() OB=3,
OB=3,
∴BH=![]() ,
,
∴BG=2BH=![]() ,
,
此时重叠部分的面积S=![]() =
=![]() ;
;
综上,重叠部分的面积为9![]() cm2或(
cm2或(![]() )cm2.
)cm2.
【解析】解:(1)∵DE=12,
∴OE=OD=6,
∵OC=8,
∴EC=8-6=2,
∴t=2![]() 2=1,
2=1,
∴当t=1时,⊙O与AC所在直线第一次相切;
如图1,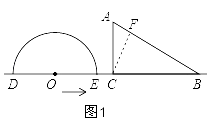
过点C作CF⊥AB于F,
在Rt![]() BCF中,∵∠ABC=30°,BC=12,
BCF中,∵∠ABC=30°,BC=12,
∴CF=![]() BC=6,
BC=6,
所以答案是:1,6.
【考点精析】利用勾股定理的概念对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案【题目】请你用学习“一次函数”时积累的经验和方法研究函数![]() 的图象和性质,并解决问题.
的图象和性质,并解决问题.
![]() 完成下列步骤,画出函数
完成下列步骤,画出函数![]() 的图象;
的图象;
![]() 列表、填空;
列表、填空;
x |
|
|
|
| 0 | 1 | 2 | 3 |
|
y |
| 3 | ______ | 1 | ______ | 1 | 2 | 3 |
|
![]() 描点:
描点:
![]() 连线
连线
![]() 观察图象,当x______时,y随x的增大而增大;
观察图象,当x______时,y随x的增大而增大;
![]() 结合图象,不等式
结合图象,不等式![]() 的解集为______.
的解集为______.