题目内容
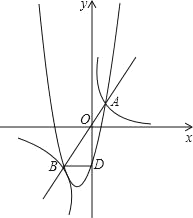
【题目】如图，直角坐标系中y＝mx和
（m＞0）图象的交点为A、B，BD⊥y轴于D，S△ABD＝4；直线A′B′由直线AB缓慢向下平移；
（1）求m的值；
（2）问直线A′B′向下平移多少单位时与经过B、D、A三点的抛物线刚好只有一个交点，并求出交点坐标．
【答案】（1）m＝4；（2）直线A′B′向下平移4个单位时，直线与抛物线只有一个交点．
【解析】
（1）根据一次函数与反比例函数的相交即可求出A，B的坐标，进而通过
进行求解即可；
（2）通过待定系数法求出抛物线解析式，进而平移后通过判别式进行判断交点的个数即可得解.
（1）∵
和
图象的交点为A，B，
∴
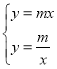，解得：
，
∴
，
，
∴
，
解得：
；
（2）由（1）可得
，
，
，
设抛物线方程为：
，
把，，分别代入解得：
，
故抛物线方程为：
，
设直线
向下平移
个单位时只有一个交点，
则平移个单位后直线的解析式为：
，
∵抛物线与直线只有一个交点，∴
，
方程可化为：
，
∴
，
∴
，
即直线向下平移4个单位时，直线与抛物线只有一个交点．
练习册系列答案
相关题目
