Question

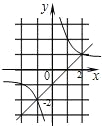如图是一次函数y=kx+b与反比例函数y=

2

x

的图象，则关于x的方程

2

x

-kx=b的解是（　　）

• A、x₁=1，x₂=2
• B、x₁=-1，x₂=-2
• C、x₁=1，x₂=-2
• D、x₁=-1，x₂=2

Answer 1

分析：先根据图示信息，观察出两图象的交点坐标；再根据函数图象交点为函数解析式组成的方程组的解来解答．

解答：解：由图象看出，一次函数y=kx+b与反比例函数y=

2

x

的图象交于点（2，1）和点（-1，-2），
方程

2

x

-kx=b变形为：

2

x

=kx+b，
即它的解为一次函数y=kx+b与反比例函数y=

2

x

的图象交点的横坐标，
∴x₁=-1，x₂=2．
故选D．

点评：本题利用了图象观察出一次函数y=kx+b与反比例函数y=

2

x

的图象的交点坐标，而方程

2

x

-kx=b的解是一次函数y=kx+b与反比例函数y=

2

x

的图象交点的横坐标．