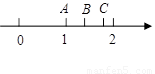题目内容
27、(1)数轴上两点表示的有理数是a、b,求这两点之间的距离;
(2)是否存在有理数x,使|x+1|+|x-3|=x?
(3)是否存在整数x,使|x-4|+|x-3|+|x+3|+|x+4|=14?如果存在,求出所有的整数x;如果不存在,说明理由.
(2)是否存在有理数x,使|x+1|+|x-3|=x?
(3)是否存在整数x,使|x-4|+|x-3|+|x+3|+|x+4|=14?如果存在,求出所有的整数x;如果不存在,说明理由.
分析:(1)数轴上两点之间的距离等于右边的数减去左边的数或|a-b|;
(2)利用绝对值的几何意义进行化简;
(3)利用绝对值的几何意义进行化简,求得|x-4|+|x-3|+|x+3|+|x+4|的最大值和最小值,再进行判断.
(2)利用绝对值的几何意义进行化简;
(3)利用绝对值的几何意义进行化简,求得|x-4|+|x-3|+|x+3|+|x+4|的最大值和最小值,再进行判断.
解答:解:(1)|a-b|;
(2)x的取值可能是x<-1,-1≤x≤3,x>3,
化简得-2x+2,4,2x-2,
则不存在|x+1|+|x-3|=x的情况;
(3)x的取值可能是x<-4,-4≤x<-3,-3≤x≤3,3<x≤4,x>4,
化简得-4x,-2x+8,14,2x+8,4x,
∴存在整数x,使|x-4|+|x-3|+|x+3|+|x+4|=14,
即-3<x≤3,x=-3,-2,-1,0,1,2,3.
(2)x的取值可能是x<-1,-1≤x≤3,x>3,
化简得-2x+2,4,2x-2,
则不存在|x+1|+|x-3|=x的情况;
(3)x的取值可能是x<-4,-4≤x<-3,-3≤x≤3,3<x≤4,x>4,
化简得-4x,-2x+8,14,2x+8,4x,
∴存在整数x,使|x-4|+|x-3|+|x+3|+|x+4|=14,
即-3<x≤3,x=-3,-2,-1,0,1,2,3.
点评:本题考查了绝对值的性质,几何意义,分情况进行讨论,有一定的难度.

练习册系列答案
相关题目
下列说法错误的是( )
| A、零是最小的整数 | ||
| B、有最大的负整数,没有最大的正整数 | ||
C、数轴上两点表示的数分别是-2
| ||
| D、所有的有理数都可以用数轴上的点表示出来 |
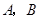 两点表示的数分别为
两点表示的数分别为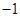 和
和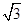 ,点B到A的距离与点C到A的距离相等,则点C所表示的数为___________
,点B到A的距离与点C到A的距离相等,则点C所表示的数为___________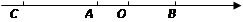
 两点表示的数分别是1和
两点表示的数分别是1和 ,点
,点 关于点
关于点 的对称点是点
的对称点是点 ,则点
,则点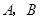 两点表示的数分别是1和
两点表示的数分别是1和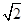 ,点关于点 的对称点是点,则点所表示的数是
.
,点关于点 的对称点是点,则点所表示的数是
.