��Ŀ����
��1����20�����ӣ���ÿ��25ǧ��Ϊ�������������ǧ�����ֱ���������������ʾ����¼���£�

��20�������У����ص�һ��������һ����ض���ǧ�ˣ�
����������Ƚϣ�20�������ܼƳ����������ǧ�ˣ�
��������ÿǧ���ۼ�2.6Ԫ���������20�����ӿ�������Ԫ�����������������
��2��̽�����ɣ� �۲�������ɵ�ͼ������ʽ��
������⣺1+3=4=22
1+3+5=9=32
1+3+5+7+9=25=52
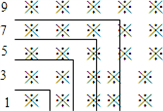
�������1+3+5+7+9+��+19=�� ����
�������1+3+5+7+9+��+��2n��1++��2n+1��+��2n+3��=�� ����
����������Ƚϣ�20�������ܼƳ����������ǧ�ˣ�
��������ÿǧ���ۼ�2.6Ԫ���������20�����ӿ�������Ԫ�����������������
��2��̽�����ɣ� �۲�������ɵ�ͼ������ʽ��
������⣺1+3=4=22
1+3+5=9=32
1+3+5+7+9=25=52
�������1+3+5+7+9+��+19=�� ����
�������1+3+5+7+9+��+��2n��1++��2n+1��+��2n+3��=�� ����
�⣺��1����2.5������3��=5.5��ǧ�ˣ���
�ڸ��ݱ���ã� ����3����1+����2����4+����1.5����2+0��3+1��2+2.5��8
=��3��8��3+0+2+20
=[����3��+����8��+����3��]+��2+20��=����14��+22=8��
�����ܼƳ���������8ǧ�ˣ�
��2.6����25��20+8��=1320.8��1321��Ԫ��
��2���ٴ�1��19����������Ϊ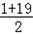 =10����
=10����
��1+3+5+7+9+��+19=102��
�ڴ�1��2n+3����������Ϊ�� =n+2��
=n+2��
��1+3+5+7+9+��+��2n��1��+��2n+1��+��2n+3��=��n+2��2��
�ʴ�Ϊ����102���ڣ�n+2��2��
�ڸ��ݱ���ã� ����3����1+����2����4+����1.5����2+0��3+1��2+2.5��8
=��3��8��3+0+2+20
=[����3��+����8��+����3��]+��2+20��=����14��+22=8��
�����ܼƳ���������8ǧ�ˣ�
��2.6����25��20+8��=1320.8��1321��Ԫ��
��2���ٴ�1��19����������Ϊ
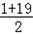 =10����
=10������1+3+5+7+9+��+19=102��
�ڴ�1��2n+3����������Ϊ��
 =n+2��
=n+2����1+3+5+7+9+��+��2n��1��+��2n+1��+��2n+3��=��n+2��2��
�ʴ�Ϊ����102���ڣ�n+2��2��

��ϰ��ϵ�д�
 ����˼ά�żӿ���ϵ�д�
����˼ά�żӿ���ϵ�д� �����Ծ�ϵ�д�
�����Ծ�ϵ�д� �ο�����������100��ϵ�д�
�ο�����������100��ϵ�д�
�����Ŀ
��1����20�����ӣ���ÿ��25ǧ��Ϊ�������������ǧ�����ֱ���������������ʾ����¼���£�
��20�������У����ص�һ��������һ����ض���ǧ�ˣ�
����������Ƚϣ�20�������ܼƳ����������ǧ�ˣ�
��������ÿǧ���ۼ�2.6Ԫ���������20�����ӿ�������Ԫ�����������������
��2��̽�����ɣ�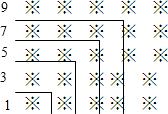
�۲�������ɵ�ͼ������ʽ��������⣺
1+3=4=22
1+3+5=9=32
1+3+5+7+9=25=52
�������1+3+5+7+9+��+19= ��
�������1+3+5+7+9+��+��2n-1��+��2n+1��+��2n+3��= ��
| ��������IJ�ֵ����λ��ǧ�ˣ� | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
| �� �� | 1 | 4 | 2 | 3 | 2 | 8 |
����������Ƚϣ�20�������ܼƳ����������ǧ�ˣ�
��������ÿǧ���ۼ�2.6Ԫ���������20�����ӿ�������Ԫ�����������������
��2��̽�����ɣ�

�۲�������ɵ�ͼ������ʽ��������⣺
1+3=4=22
1+3+5=9=32
1+3+5+7+9=25=52
�������1+3+5+7+9+��+19=
�������1+3+5+7+9+��+��2n-1��+��2n+1��+��2n+3��=
��20������,��ÿ��25ǧ��Ϊ��,���������ǧ�����ֱ���������������ʾ,��¼����:
|
��������IJ�ֵ (��λ:ǧ��) |
|
|
|
0 |
1 |
2.5 |
|
���� |
1 |
4 |
2 |
3 |
2 |
8 |
(1)20��������,���ص�һ��������һ����ض���ǧ��?
(2)��������Ƚ�,20�������ܼƳ����������ǧ��?
(3)������ÿǧ���ۼ�2.6Ԫ,�������20�����ӿ�������Ԫ?(�����������)
��20������,��ÿ��25ǧ��Ϊ��,���������ǧ�����ֱ���������������ʾ,��¼����:
|
��������IJ�ֵ (��λ:ǧ��) |
|
|
|
0 |
1 |
2.5 |
|
���� |
1 |
4 |
2 |
3 |
2 |
8 |
(1)20��������,���ص�һ��������һ����ض���ǧ��?
(2)��������Ƚ�,20�������ܼƳ����������ǧ��?
(3)������ÿǧ���ۼ�2.6Ԫ,�������20�����ӿ�������Ԫ?(�����������)

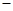 3
3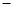 3
3