Question

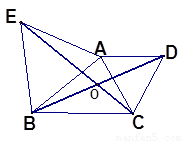
如图，△ABC的两边AB和AC的垂直平分线分别交BC于D，E，若∠BAC+∠DAE=150°，则∠BAC的度数是（       ）.

(A) 105°        (B) 110°       (C) 115°        (D) 120°

 

Answer 1

【答案】

B

【解析】

试题分析：根据垂直平分线性质：垂直平分线上的点到线段两段的距离相等，可得DA=DB，EA=EC，再根据等角对等边可得∠B=∠DAB，∠C=∠EAC，则有∠B+∠C+2∠DAE=150°，即 180°-∠BAC+2∠DAE=150°，再与∠BAC+∠DAE=150°联立解方程组即可．

∵△ABC的两边AB，AC的垂直平分线分别交BC于D，E，

∴DA=DB，EA=EC，

∴∠B=∠DAB，∠C=∠EAC．

∵∠BAC+∠DAE=150°，①

∴∠B+∠C+2∠DAE=150°．

∵∠B+∠C+∠BAC=180°，

∴180°-∠BAC+2∠DAE=150°，

即∠BAC-2∠DAE=30°．②

由①②组成的方程组：

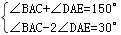
解得∠BAC=110°，

故选B.

考点：此题考查了线段的垂直平分线、等腰三角形的性质、三角形内角和定理

点评：本题主要考查的是线段垂直平分线的性质及等腰三角形的性质，三角形的内角和定理知识点的理解和掌握，能综合运用这些性质进行计算是解此题的关键．