题目内容
23、甲车从A地出发以60km/h的速度沿公路匀速行驶.0.5小时后，乙车也从A地出发，以80km/h的速度沿该公路与甲车同向匀速行驶．
（1）设乙车出发之后行驶的时间为x（小时），分别写出甲车、乙车行驶路程y1、y2（千米）与乙车行驶时间x（小时）之间的函数关系式；
（2）利用（1）中建立的函数关系式，求乙车出发后几小时追上甲车．
（1）设乙车出发之后行驶的时间为x（小时），分别写出甲车、乙车行驶路程y1、y2（千米）与乙车行驶时间x（小时）之间的函数关系式；
（2）利用（1）中建立的函数关系式，求乙车出发后几小时追上甲车．
分析：（1）根据路程=速度×时间建立关系式；
（2）乙追上甲即y2=y1，列方程求解．
（2）乙追上甲即y2=y1，列方程求解．
解答：解：（1）甲车行驶路程y1与乙车行驶时间x（小时）之间的函数关系式为：y1=60x+30；（2分）
乙车行驶路程y2与乙车行驶时间x（小时）之间的函数关系式为：y2=80x．（2分）
（2）依据题意，得 80x=60x+30，（2分）
解得 x=1.5． （1分）
答：甲车、乙车行驶路程y1、y2（千米）与乙车行驶时间x（小时）之间的函数关系式分别为y1=60x+30，y2=80x；乙车出发1.5小时后追上甲车．（1分）
乙车行驶路程y2与乙车行驶时间x（小时）之间的函数关系式为：y2=80x．（2分）
（2）依据题意，得 80x=60x+30，（2分）
解得 x=1.5． （1分）
答：甲车、乙车行驶路程y1、y2（千米）与乙车行驶时间x（小时）之间的函数关系式分别为y1=60x+30，y2=80x；乙车出发1.5小时后追上甲车．（1分）
点评：此题考查一次函数的应用，难度不大．
练习册系列答案
相关题目
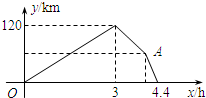车之间的距离y（km）与乙车行驶时间x（h）之间的函数图象．以下结论正确的是