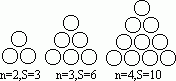题目内容
如图所示，下列每个图是由若干盆花组成的形如三角形的图案，每条边（包括两个顶点）有n盆花，每个图案花盆总数是S，按此推断S与n的关系式为（ ）
分析：由图可知：
第一图：有花盆3个，每条边有2盆花，那么3=3×（2-1）；
第二图：有花盆6个，每条边有3盆花，那么6=3×（3-1）；
第三图：有花盆9个，每条边有4盆花，那么9=3×（4-1）；
…
由此可知S与n的关系式为S=3（n-1）．
第一图：有花盆3个，每条边有2盆花，那么3=3×（2-1）；
第二图：有花盆6个，每条边有3盆花，那么6=3×（3-1）；
第三图：有花盆9个，每条边有4盆花，那么9=3×（4-1）；
…
由此可知S与n的关系式为S=3（n-1）．
解答：解：根据图案组成的是三角形的形状，则其周长等于边长的3倍，但由于每个顶点重复了一次．
所以S=3n-3，即S=3（n-1）．
故选B．
所以S=3n-3，即S=3（n-1）．
故选B．
点评：本题是一道找规律的题目，这类题型在中考中经常出现．本题要注意给出的图片中所包含的规律，然后根据规律列出函数关系式．
练习册系列答案
相关题目
