题目内容
某班50名同学分别站在公路的A，B两点处，A，B两点相距1000米，A处有30人，B处有20人，要让两处的同学走到一起，并且使所有同学走的路程总和最小，那么集合地点应选在（ ）| A、A点处 | ||
| B、线段AB的中点处 | ||
C、线段AB上，距A点
| ||
| D、线段AB上，距A点400米处 |
分析：设A处学生走的路程，表示出B处学生走的路程，然后列式计算所有同学走的路程之和．
解答：解：设A处的同学走x米，那么B处的同学走（1000-x）米，
所有同学走的路程总和：
L=30x+20（1000-x）=10x+20000
此时0≤x≤1000，要使L最小，必须x=0，
此时L最小值为20000；
所以选A点处．
故选A．
所有同学走的路程总和：
L=30x+20（1000-x）=10x+20000
此时0≤x≤1000，要使L最小，必须x=0，
此时L最小值为20000；
所以选A点处．
故选A．
点评：此题主要考查一次函数在实际生活中的意义，学生在学这一部分时一定要联系实际，不能死学．
练习册系列答案
相关题目
某班50名同学分别站在同一公路上相距1000米的M、N两点处，M处有30人，N处有20人，要让两处的同学集合到一起，并且使所有同学走的路程总和最小，那么集合地点应选在
| A．M 点处 | B．N点处 |
| C．线段MN的中点处 | D．线段MN上，距M点400米处 |
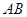的中点处
米处 