题目内容
下表给出了代数式x2+bx+c与x的一些对应值：| x | … | -1 | 1 | 2 | 3 | 4 | … | |
| X2+bx+c | … | 3 | -1 | 3 | … |
（2）代数式x2+bx+c是否有最小值？如果有，求出最小值；如果没有，请说明理由；
（3）设y=x2+bx+c的图象与x轴的交点为A、B两点（A点在B点左侧），与y轴交于点C，P点为线段AB上一动点，过P点作PE∥AC交BC于E，连接PC，当△PEC的面积最大时，求P点的坐标．
【答案】分析：（1）根据图表中已知的三组数据，用待定系数法即可求出b、c的值；进而可由抛物线的解析式填齐空白处的对应值；
（2）根据（1）所得函数的解析式，可用配方法或公式法求出其最小值；
（3）由于△PEC的面积无法直接得出，所以要转化为其他图形面积的和差来解；可设出P点的坐标，过E作EM⊥x轴于M，易证得△BPE∽△BAC，那么它们的对应高等于相似比，由此可求出EM的表达式；那么△PEC的面积可由△ABC、△BPE、△APC的面积差求得，也就得到了关于△PEC的面积与P点横坐标的函数关系式，根据函数的性质即可求出S的最大值及对应的P点坐标．
解答：解：（1）由题意知：
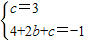解得b=-4（1分）
（2）∵x2-4x+3=（x-2）2-1≥-1
∴x2-4x+3有最小值，最小值为-1；（3分）
（3）由（1）可知，点A、B的坐标分别为（1，0），（3，0）、设点P的坐标为（x，0），过点E作EM⊥x轴于点M，
∵PE∥AC，∴△EPB∽△CAB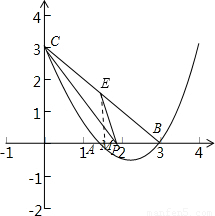
∵EM、CO分别为△EPB与△CAB边上的高，
∴
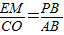（4分）
∵CO=3，AB=2，PB=3-x，∴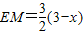
（5分）
∴S△PEC=S△PBC-S△PBE=
PB•CO-
PB•EM（6分）
=
=
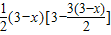（7分）
∴当x=2时，S有最大值
；
∴当点P的坐标为（2，0）时，△PEC的面积最大．（8分）
点评：此题主要考查了用待定系数法求二次函数解析式、相似三角形的判定和性质、图形面积的求法及二次函数的应用等，综合性较强，难度偏大．
（2）根据（1）所得函数的解析式，可用配方法或公式法求出其最小值；
（3）由于△PEC的面积无法直接得出，所以要转化为其他图形面积的和差来解；可设出P点的坐标，过E作EM⊥x轴于M，易证得△BPE∽△BAC，那么它们的对应高等于相似比，由此可求出EM的表达式；那么△PEC的面积可由△ABC、△BPE、△APC的面积差求得，也就得到了关于△PEC的面积与P点横坐标的函数关系式，根据函数的性质即可求出S的最大值及对应的P点坐标．
解答：解：（1）由题意知：
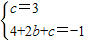解得b=-4（1分）| x | … | -1 | 1 | 2 | 3 | 4 | … | |
| X2+bx+c | … | 8 | 3 | 0 | -1 | 0 | 3 | … |
∴x2-4x+3有最小值，最小值为-1；（3分）
（3）由（1）可知，点A、B的坐标分别为（1，0），（3，0）、设点P的坐标为（x，0），过点E作EM⊥x轴于点M，
∵PE∥AC，∴△EPB∽△CAB
∵EM、CO分别为△EPB与△CAB边上的高，
∴
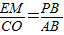（4分）∵CO=3，AB=2，PB=3-x，∴
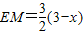（5分）∴S△PEC=S△PBC-S△PBE=
PB•CO-PB•EM（6分）=
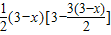=（7分）∴当x=2时，S有最大值
；∴当点P的坐标为（2，0）时，△PEC的面积最大．（8分）
点评：此题主要考查了用待定系数法求二次函数解析式、相似三角形的判定和性质、图形面积的求法及二次函数的应用等，综合性较强，难度偏大．
练习册系列答案
相关题目
下表给出了代数式x2+bx+c与x的一些对应值：
（1）请在表内的空格中填入适当的数；
（2）设y=x2+bx+c，则当x取何值时，y＞0；
（3）请说明经过怎样平移函数y=x2+bx+c的图象得到函数y=x2的图象？
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| x2+bx+c | … | 3 | -1 | 3 | … |
（2）设y=x2+bx+c，则当x取何值时，y＞0；
（3）请说明经过怎样平移函数y=x2+bx+c的图象得到函数y=x2的图象？
下表给出了代数式x2+bx+c与x的一些对应值：
（1）根据表格中的数据，确定b、c的值，并填齐表格空白处的对应值；
（2）设y=x2+bx+c的图象与x轴的交点为A、B两点（A点在B点左侧），与y轴交于点C，P为线段AB上一动点，过P点作PE∥AC交BC于E，连接PC，当△PEC的面积最大时，求P点的坐标．
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| x2+bx+c | … | 3 | -1 | 3 | … |
（2）设y=x2+bx+c的图象与x轴的交点为A、B两点（A点在B点左侧），与y轴交于点C，P为线段AB上一动点，过P点作PE∥AC交BC于E，连接PC，当△PEC的面积最大时，求P点的坐标．
下表给出了代数式x2+bx+c与x的一些对应值：
（1）根据表格中的数据，确定b、c的值，并填齐表格中空白处的对应值；
（2）代数式x2+bx+c是否有最小值？如果有，求出最小值；如果没有，请说明理由；
（3）设y=x2+bx+c的图象与x轴的交点为A、B两点（A点在B点左侧），与y轴交于点C，P点为线段AB上一动点，过P点作PE∥AC交BC于E，连接PC，当△PEC的面积最大时，求P点的坐标．
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| X2+bx+c | … | 3 | -1 | 3 | … |
（2）代数式x2+bx+c是否有最小值？如果有，求出最小值；如果没有，请说明理由；
（3）设y=x2+bx+c的图象与x轴的交点为A、B两点（A点在B点左侧），与y轴交于点C，P点为线段AB上一动点，过P点作PE∥AC交BC于E，连接PC，当△PEC的面积最大时，求P点的坐标．
下表给出了代数式x2+bx+c与x的一些对应值：
函数y=x2的图象可以通过平移得到函数y=x2+bx+c的图象．请写出一种正确的平移 ．
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| x2+bx+c | … | 3 | -1 | 3 | … |