题目内容
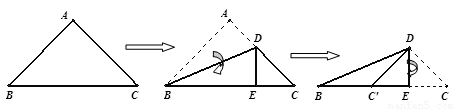
如图,将一个等腰直角三角形按图示方式依次翻折,则下列说法:①DC′平分∠BDE;②△BC′D是等腰三角形;③△CED的周长等于BC的长;④BD=2DE中正确的个数有( )


分析:根据折叠的性质可得出∠DBC=22.5°,△DEC和△DEC'均是等腰直角三角形,结合选项所述即可判断出正确与否.
解答:解:(1)由折叠的性质得,∠BDC′=22.5°,∠C′DE=∠CDE=45°,
∴DC′不平分∠BDE
故①错误;
(2)∵∠ABC=2∠DBC,
∴∠DBC=22.5°,∠DC′C=∠DCB=45°=∠DBC′+∠BDC′,
∴∠DBC′=∠BDC′=22.5°,
∴BC′=DC′,
故②正确;
(3)由折叠的性质可得出△DEC和△DEC'均是等腰直角三角形,
又∵BC′=DC′,
∴△CED的周长=CE+DE+CD=CE+C′E+BC′=BC,
故③正确.
(4)由折叠的性质得,∠DBC=22.5°≠30°,
∴BD≠2DE.
综上可得②③正确,共两个.
故选B.
∴DC′不平分∠BDE
故①错误;
(2)∵∠ABC=2∠DBC,
∴∠DBC=22.5°,∠DC′C=∠DCB=45°=∠DBC′+∠BDC′,
∴∠DBC′=∠BDC′=22.5°,
∴BC′=DC′,
故②正确;
(3)由折叠的性质可得出△DEC和△DEC'均是等腰直角三角形,
又∵BC′=DC′,
∴△CED的周长=CE+DE+CD=CE+C′E+BC′=BC,
故③正确.
(4)由折叠的性质得,∠DBC=22.5°≠30°,
∴BD≠2DE.
综上可得②③正确,共两个.
故选B.
点评:本题考查了折叠的性质,注意掌握折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等,难度一般.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目



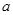 ,则①DC′平分∠BDE;②BC长为
,则①DC′平分∠BDE;②BC长为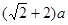 ;③△B
C′D是等腰三角形;④△CED的周长等于BC的长.则上述命题中正确是___________(填序号);
;③△B
C′D是等腰三角形;④△CED的周长等于BC的长.则上述命题中正确是___________(填序号);