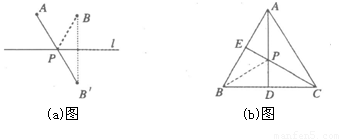题目内容
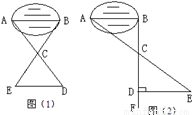
(本小题满分12分)某班同学到野外活动,为测量一池塘两端A、B的距离,设计了几种方案,下面介绍两种:(I)如图(1),先在平地取一个可以直接到达A、B的点C,并分别延长AC到D,BC到E,使DC=AC,BC=EC,最后测出DE的距离即为AB的长。(II)如图(2),先过B点作AB的垂线BF,再在BF上取C、D两点,使BC=CD,接着过点D作BD的垂线DE,交AC的延长线于E,则测出DE的长即为AB的距离。阅读后回答下列问题:

1.(1)方案(I)是否可行?为什么?
2.(2)方案(II)是否切实可行?为什么?
3.(3)方案(II)中作BF⊥AB,ED⊥BF的目的是 ;若仅满足∠ABD=∠BDE≠90°,方案(II)是否成立?
4.(4)方案(II)中,若使BC=n·CD,能否测得(或求出)AB的长?理由是 ,若ED=m,则AB= 。
1.(1)方案(I)可行;
∵DC=AC,EC=BC且有对顶角∠ACB=∠DCE,
∴△ACB≌△DCE(SAS), ∴AB=DE,
∴测出DE的距离即为AB的长。故方案(I)可行。(3分)
2.(2)方案(II)可行;
∵AB⊥BC,DE⊥CD, ∴∠ABC=∠EDC=90°,
又∵BC=CD,∠ACB=∠ECD,∴△ABC≌△EDC, ∴AB=ED,
∴测出DE的长即为AB的距离。故方案(II)可行。(6分)
3.(3)方案(II)中作BF⊥AB,ED⊥BF的目的是作直角三角形;
若∠ABD=∠BDE≠90°,∠ACB=∠ECD, ∴△ABC∽△EDC,
∴![]() , ∴只要测出ED、BC、CD的长,即可求得AB的长。
, ∴只要测出ED、BC、CD的长,即可求得AB的长。
∴ED的长不等于AB的长,∴方案(II)不成立。(9分)
4.(4)根据(3)中所求可以得出,∴![]() , ∵BC=n•CD,
, ∵BC=n•CD,
∴ ABED=n,求出DE即可得出答案,
当ED=m,则AB=mn。(12分)
解析:略

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案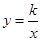 的图象经过A、B两点,根据图中信息解答下列问题:
的图象经过A、B两点,根据图中信息解答下列问题: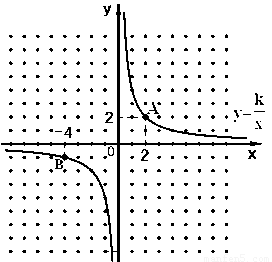

 同侧,在直线
同侧,在直线 ,连接
,连接 ,与直线
,与直线