题目内容
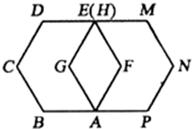
如图,如果边长为1的正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合,那么点B的对应点是点 ,点E在整个旋转过程中,所经过的路径长为 (结果保留π).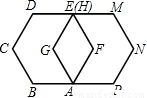
【答案】分析:根据图形旋转的性质接可求出点B的对应点,再连接AE,过F点像AE作垂线,利用锐角三角函数的定义及直角三角形的性质可求出AE的长,再利用弧长公式接可求出E在整个旋转过程中,所经过的路径长.
解答: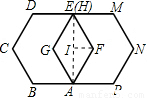 解:∵六边形ABCDEF是正六边形,
解:∵六边形ABCDEF是正六边形,
∴此六边形的各内角是120°,
∵正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合,
∴B点只能与G点重合,
连接AE,过F点向AE作垂线,垂足为I,
∵EF=AF=1,IF⊥AE,
∴AE=2EI,
∵∠AFE=120°,
∴∠EFI=60°,
∴EI=EF•sin60°=1×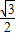 =
=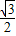 ,
,
∴AE=2×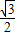 =
=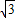 ,
,
∴E点所经过的路线是以A为圆心,以AE为半径,圆心角为60度的一段弧,
∴E在整个旋转过程中,所经过的路径长=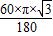 =
=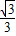 π.
π.
故答案为:G、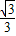 π.
π.
点评:本题考查的是图形旋转的性质、正多边形和圆及弧长的计算、等腰三角形的性质,根据题意作出辅助线,构造出等腰三角形是解答此题的关键.
解答:
 解:∵六边形ABCDEF是正六边形,
解:∵六边形ABCDEF是正六边形,∴此六边形的各内角是120°,
∵正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合,
∴B点只能与G点重合,
连接AE,过F点向AE作垂线,垂足为I,
∵EF=AF=1,IF⊥AE,
∴AE=2EI,
∵∠AFE=120°,
∴∠EFI=60°,
∴EI=EF•sin60°=1×
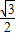 =
=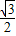 ,
,∴AE=2×
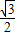 =
=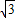 ,
,∴E点所经过的路线是以A为圆心,以AE为半径,圆心角为60度的一段弧,
∴E在整个旋转过程中,所经过的路径长=
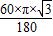 =
=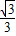 π.
π.故答案为:G、
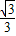 π.
π.点评:本题考查的是图形旋转的性质、正多边形和圆及弧长的计算、等腰三角形的性质,根据题意作出辅助线,构造出等腰三角形是解答此题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
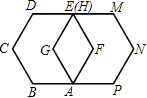 如图,如果边长为1的正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合,那么点B的对应点是点
如图,如果边长为1的正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合,那么点B的对应点是点 如图,如果边长为1的等边△PQR沿着边长为1的正方形ABCD的外部的边如图位置开始顺时针连续滚动,当它滚动121次时,点P所经过的路程是
如图,如果边长为1的等边△PQR沿着边长为1的正方形ABCD的外部的边如图位置开始顺时针连续滚动,当它滚动121次时,点P所经过的路程是