题目内容
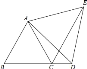
【题目】（阅读）如图1，等边△ABC中，P是AC边上一点，Q是CB延长线上一点，若AP＝BQ．则过P作PF∥BC交AB于F，可证△APF是等边三角形，再证△PDF≌QDB可得D是FB的中点．请写出证明过程．
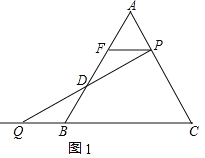
（运用）如图2，△ABC是边长为6的等边三角形，P是AC边上一动点，由A向C运动（与A，C不重合），Q是CB延长线上一动点，与点P同时以相同的速度由B向CB延长线方向运动（Q不与B重合），过P作PE⊥AB于E，连接PQ交AB于D．
（1）当∠BQD＝30°时，求AP的长；
（2）在运动过程中线段ED的长是否发生变化？如果不变，直接写出线段ED的长；如果发生改变，请说明理由．
【答案】“阅读”详见解析；“运用”（1）AP＝2；（2）运动过程中线段ED的长始终为3．
【解析】
【阅读】
：由△ABC是等边三角形和PF∥BC可得PF＝BQ，进而证△PFD≌△QBD得DF＝DB．
【运用】：（1）由△ABC是边长为6的等边三角形，可知∠ACB=60°，再由∠BQD=30°可知∠QPC=90°，设AP=x，则PC=6-x，QB=x，在Rt△QCP中，∠BQD=30°，PC=
QC，即6-x=（6+x），求出x的值即可；
（2）作QG⊥AB，交直线AB于点G，连接QE，PG，由点P、Q做匀速运动且速度相同，可知AP=BQ，再根据全等三角形的判定定理得出△APE≌△BQG，再由AE=BG，PE=QG且PE∥QG，可知四边形PEQG是平行四边形，进而可得出EB+AE=BE+BG=AB，DE=AB，由等边△ABC的边长为6，可得出DE=3．
解：【阅读】证明：如图1中，
∵△ABC是等边三角形，
∴∠ABC＝∠ACB＝60°，
∵PF∥BC，
∴∠AFP＝∠APF＝∠ABC＝∠ACB＝60°，
∴AP＝PF，
∵AP＝BQ，
∴PF＝BQ，
∵PF∥BQ，
∴∠FPD＝∠DQB，∠PFD＝∠QBD，
在△PFD与△QBD中，
，
∴△PFD≌△QBD；
∴DF＝DB．
【运用】
：解：（1）如图2中，
∵△ABC是边长为6的等边三角形，
∴∠ACB＝60°，
∵∠BQD＝30°，
∴∠QPC＝90°，
设AP＝x，则PC＝6﹣x，QB＝x，
∴QC＝QB+BC＝6+x，
∵在Rt△QCP中，∠BQD＝30°，
∴PC＝QC，即6﹣x＝（6+x），解得x＝2，
∴AP＝2；
（2）作QG⊥AB，交直线AB于点G，连接QE，PG，
又∵PE⊥AB于E，
∴∠PGQ＝∠AEP＝90°，
∵点P、Q速度相同，
∴AP＝BQ，
∵△ABC是等边三角形，
∴∠A＝∠ABC＝∠GBQ＝60°，
在△APE和△BQG中，
∵∠AEP＝∠BGQ＝90°，
∴∠APE＝∠BQG，
，
∴△APE≌△BQG（AAS），
∴AE＝BG，PE＝QG且PE∥QG，
∴四边形PEQG是平行四边形，
∴DE＝EG，
∵EB+AE＝BE+BG＝AB，
∴DE＝AB，
又∵等边△ABC的边长为6，
∴DE＝3，
故运动过程中线段ED的长始终为3．
