题目内容
如图,直线y=mx与双曲线y= 相交于A、B两点,A点的坐标为(1,2)
相交于A、B两点,A点的坐标为(1,2)
(1)求反比例函数的表达式;
(2)根据图象直接写出当mx> 时,x的取值范围;
时,x的取值范围;
(3)计算线段AB的长.

 相交于A、B两点,A点的坐标为(1,2)
相交于A、B两点,A点的坐标为(1,2)(1)求反比例函数的表达式;
(2)根据图象直接写出当mx>
 时,x的取值范围;
时,x的取值范围;(3)计算线段AB的长.

(1)反比例函数的表达式是y=;
(2)当mx>时,x的取值范围是﹣1<x<0或x>1;
(3)AB=2 .
.
(2)当mx>时,x的取值范围是﹣1<x<0或x>1;
(3)AB=2
 .
.试题分析:(1)将点A的坐标代入反比例函数的解析式即可求出;
(2)将点A的坐标代入直线的解析式可求出直线的解析式,解y=mx与y=
 组成的方程组求出B的坐标,根据A、B的坐标结合图象就可以得出;
组成的方程组求出B的坐标,根据A、B的坐标结合图象就可以得出;(3)利用勾股定理分别求出OA、OB,即可得出.
试题解析:(1)把A(1,2)代入y=
 得:k=2,
得:k=2,即反比例函数的表达式是y=
 ;
;(2)把A(1,2)代入y=mx得:m=2,
即直线的解析式是y=2x,
解方程组
 得出B点的坐标是(﹣1,﹣2),
得出B点的坐标是(﹣1,﹣2),∴当mx>
 时,x的取值范围是﹣1<x<0或x>1;
时,x的取值范围是﹣1<x<0或x>1;(3)过A作AC⊥x轴于C,
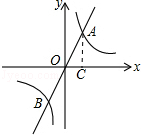
∵A(1,2),
∴AC=2,OC=1,
由勾股定理得:AO=
 ,
,同理求出OB=
 ,
,∴AB=2
 .
.
练习册系列答案
相关题目
 ,0),且与反比例函数y=
,0),且与反比例函数y= (m≠0)的图象相交于点A(﹣2,1)和点B.
(m≠0)的图象相交于点A(﹣2,1)和点B.
 2
2 图象上,求这两个函数图象的另一交点N的坐标.
图象上,求这两个函数图象的另一交点N的坐标. .我们规定:满足不等式
.我们规定:满足不等式 的实数x的所有取值的全体叫做闭区间,表示为
的实数x的所有取值的全体叫做闭区间,表示为 .对于一个函数,如果它的自变量x与函数值y满足:当
.对于一个函数,如果它的自变量x与函数值y满足:当 ,我们就称此函数是闭区间
,我们就称此函数是闭区间 是闭区间
是闭区间 上的“闭函数”吗?请判断并说明理由;
上的“闭函数”吗?请判断并说明理由; 是闭区间
是闭区间 上的“闭函数”,求此函数的解析式;
上的“闭函数”,求此函数的解析式;  ,且
,且 ,当二次函数
,当二次函数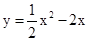 是闭区间
是闭区间 上的“闭函数”时,求c,d的值.
上的“闭函数”时,求c,d的值.
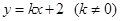 与反比例函数G1:
与反比例函数G1: 的图象交于点
的图象交于点 ,B(b,-1),与y轴交于点D.
,B(b,-1),与y轴交于点D. ,
, ,直接写出t的取值范围.
,直接写出t的取值范围.
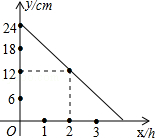
 (单位:平方米)与工作时间
(单位:平方米)与工作时间 (单位:小时)的函数关系的图象如图所示,则休息后园林队每小时绿化面积为
(单位:小时)的函数关系的图象如图所示,则休息后园林队每小时绿化面积为